山东省济宁市任城区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 抛物线 与 轴的交点坐标为( )A、 B、 C、 D、2. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则cosA的值为( )
 A、 B、 C、 D、3. 将抛物线y=2(x+1)2+1向左平移2个单位长度,再向上平移3个单位,所得到的新抛物线的顶点坐标是( )A、(1,﹣2) B、(﹣3,﹣2) C、(﹣3,4) D、(3,4)4. 如图,为方便行人过某天桥,市政府在10米高的天桥两端修建斜道,设计斜坡满足sinA= ,则斜道AC的长度是( )
A、 B、 C、 D、3. 将抛物线y=2(x+1)2+1向左平移2个单位长度,再向上平移3个单位,所得到的新抛物线的顶点坐标是( )A、(1,﹣2) B、(﹣3,﹣2) C、(﹣3,4) D、(3,4)4. 如图,为方便行人过某天桥,市政府在10米高的天桥两端修建斜道,设计斜坡满足sinA= ,则斜道AC的长度是( ) A、25 B、30 C、35 D、405. 对于反比例函数y= ,下列说法不正确的是( )A、这个函数的图象分布在第一、三象限 B、这个函数的图象既是轴对称图形又是中心对称图形 C、点(1,4)在这个函数图象上 D、当x>0时,y随x的增大而增大6. 如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( )
A、25 B、30 C、35 D、405. 对于反比例函数y= ,下列说法不正确的是( )A、这个函数的图象分布在第一、三象限 B、这个函数的图象既是轴对称图形又是中心对称图形 C、点(1,4)在这个函数图象上 D、当x>0时,y随x的增大而增大6. 如图,太阳光线与地面成80°角,窗子AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是( ) A、 米 B、 米 C、 米 D、 米7. 若点M(﹣1,y1),N(1,y2),P( ,y3)都在抛物线y=﹣x2+4x+m2+1上,则y1 , y2 , y3大小关系为( )A、y3<y1<y2 B、y1<y3<y2 C、y2<y1<y3 D、y2<y3<y18. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点 ,以 为边作平行四边形 ,其中 , 在 轴上,则 为( )
A、 米 B、 米 C、 米 D、 米7. 若点M(﹣1,y1),N(1,y2),P( ,y3)都在抛物线y=﹣x2+4x+m2+1上,则y1 , y2 , y3大小关系为( )A、y3<y1<y2 B、y1<y3<y2 C、y2<y1<y3 D、y2<y3<y18. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点 ,以 为边作平行四边形 ,其中 , 在 轴上,则 为( )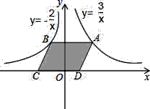 A、2 B、3 C、4 D、59. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c>0;④当x<0时,y随x增大而增大,其中结论正确的个数是( )
A、2 B、3 C、4 D、59. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③3a+c>0;④当x<0时,y随x增大而增大,其中结论正确的个数是( ) A、4个 B、3个 C、2个 D、1个10. 如图.抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集为( )
A、4个 B、3个 C、2个 D、1个10. 如图.抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2+mx+c>n的解集为( )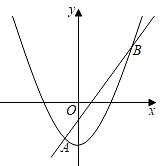 A、x>﹣1 B、x<3 C、x<﹣3或x>1 D、﹣1<x<3
A、x>﹣1 B、x<3 C、x<﹣3或x>1 D、﹣1<x<3二、填空题
-
11. 二次函数 的顶点坐标是 .12. 如题图,反比例函数y= 的图象与一次函数y=x+2的图象交于点A(1,m),则反比例函数y= 的表达式为 .
 13. 如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上则tanA的值为 .
13. 如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上则tanA的值为 . 14. 开口向上的抛物线y=a(x+2)(x-8)与x轴交于A,B两点,与y轴交于点C,若∠ACB=90°,则a=.15. 如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y= (k>0,x>0)的图象上,已知A、B的横坐标分别为1、4,且对角线BD∥x轴,若菱形ABCD的面积为30,则k的值为 .
14. 开口向上的抛物线y=a(x+2)(x-8)与x轴交于A,B两点,与y轴交于点C,若∠ACB=90°,则a=.15. 如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y= (k>0,x>0)的图象上,已知A、B的横坐标分别为1、4,且对角线BD∥x轴,若菱形ABCD的面积为30,则k的值为 .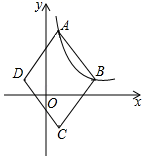
三、解答题
-
16. 2 cos 30°+tan 45- 4sin260°17. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度 与时间 之间的函数关系,其中线段 , 表示恒温系统开启阶段,双曲线的一部分 表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)、求 与 ( )的函数表达式;(2)、若大棚内的温度低于 时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害? 18. 河上有一座桥孔为抛物线形的拱桥,水面宽6m时,水面离桥孔顶部3m.因降暴雨水位上升lm.
18. 河上有一座桥孔为抛物线形的拱桥,水面宽6m时,水面离桥孔顶部3m.因降暴雨水位上升lm.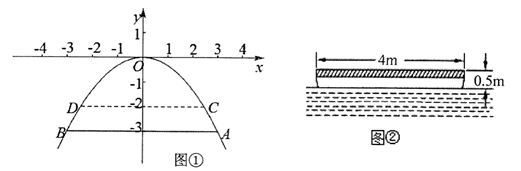 (1)、如图①,若以桥孔的最高点为原点,建立平面直角坐标系,求抛物线的解析式;(2)、一艘装满物资的小船,露出水面的高为0.5m、宽为4m(横断面如图②).暴雨后这艘船能从这座拱桥下通过吗?请说明理由.19. 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°.若已知旗杆的高度AB=5米,求建筑物BC的高度.(参考数据:sin50°≈0.8,tan50°≈1.2)
(1)、如图①,若以桥孔的最高点为原点,建立平面直角坐标系,求抛物线的解析式;(2)、一艘装满物资的小船,露出水面的高为0.5m、宽为4m(横断面如图②).暴雨后这艘船能从这座拱桥下通过吗?请说明理由.19. 测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°.若已知旗杆的高度AB=5米,求建筑物BC的高度.(参考数据:sin50°≈0.8,tan50°≈1.2) 20. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费80元时,床位可全部租出,若每张床位每天收费提高10元,则相应的减少了10张床位租出,如果每张床位每天以10元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天应提高多少元?21. 如图,点O是坐标原点,△OBA∽△DOC,边OA、OC都在x轴的正半轴上.已知点B的坐标为(12,16),∠BAO=∠OCD=90°,OD=10,反比例函数的图象经过点D,交AB边于点E.
20. 某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费80元时,床位可全部租出,若每张床位每天收费提高10元,则相应的减少了10张床位租出,如果每张床位每天以10元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天应提高多少元?21. 如图,点O是坐标原点,△OBA∽△DOC,边OA、OC都在x轴的正半轴上.已知点B的坐标为(12,16),∠BAO=∠OCD=90°,OD=10,反比例函数的图象经过点D,交AB边于点E. (1)、求该反比例函数的解析式;(2)、求BE的长.22. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35m的速度沿着与水平方向成75°角的方向飞行,40min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高( ≈1.4, ≈1.7, ≈2.45,结果精确到个位).
(1)、求该反比例函数的解析式;(2)、求BE的长.22. 如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35m的速度沿着与水平方向成75°角的方向飞行,40min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高( ≈1.4, ≈1.7, ≈2.45,结果精确到个位). 23. 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,点P是抛物线上一动点,连接PB,PC.
23. 如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,点P是抛物线上一动点,连接PB,PC. (1)、求抛物线的解析式;(2)、如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;(3)、抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.
(1)、求抛物线的解析式;(2)、如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;(3)、抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.