山东省济宁市曲阜市2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下列方程属于一元二次方程的是( )A、x2+y+2=0 B、x+y=5 C、x+ =5 D、x2+2x=32. 对称美是美的一种重要形式,它能给与人们一种圆满、协调和平的美感,下列图形属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将抛物线 向下平移两个单位,以下说法错误的是( )A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变4. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( )
3. 将抛物线 向下平移两个单位,以下说法错误的是( )A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变4. 如图, 是 的直径, 是 的弦.若 ,则 的度数是( ) A、 B、 C、 D、5. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、6. 已知点A(3,y1),B(4,y2),C(﹣3,y3)均在抛物线y=2x2﹣4x+m上,下列说法中正确的是( )A、y3<y2<y1 B、y2<y1<y3 C、y3<y1<y2 D、y1<y2<y37. 如图,在 中, , ,将三角形ABC绕点A按顺时针方向旋转到三角形 的位置,使得点 、 、 在一条直线上,那么旋转角等于( )
A、 B、 C、 D、5. 用配方法解方程 ,配方后所得的方程是( )A、 B、 C、 D、6. 已知点A(3,y1),B(4,y2),C(﹣3,y3)均在抛物线y=2x2﹣4x+m上,下列说法中正确的是( )A、y3<y2<y1 B、y2<y1<y3 C、y3<y1<y2 D、y1<y2<y37. 如图,在 中, , ,将三角形ABC绕点A按顺时针方向旋转到三角形 的位置,使得点 、 、 在一条直线上,那么旋转角等于( ) A、145° B、130° C、135° D、125°8. 某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )A、 B、 C、 D、9. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心 为圆心的圆,如图2,已知圆心 在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点 为运行轨道的最低点,则点 到弦 所在直线的距离是( )
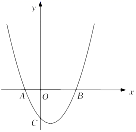
A、145° B、130° C、135° D、125°8. 某蔬菜种植基地2018年的蔬菜产量为800吨,2020年的蔬菜产量为968吨,设每年蔬菜产量的年平均增长率都为x,则年平均增长率x应满足的方程为( )A、 B、 C、 D、9. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心 为圆心的圆,如图2,已知圆心 在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点 为运行轨道的最低点,则点 到弦 所在直线的距离是( ) A、1米 B、 米 C、2米 D、 米10. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①a>0;②b2﹣4ac>0;③4a+b=1;④不等式ax2+(b﹣1)x+c<0的解集为1<x<3,正确的结论个数是( )
A、1米 B、 米 C、2米 D、 米10. 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①a>0;②b2﹣4ac>0;③4a+b=1;④不等式ax2+(b﹣1)x+c<0的解集为1<x<3,正确的结论个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知一元二次方程x2+kx-3=0有一个根为1,则k的值为.12. 请写出一个 开口向下,并且与y轴交于点(0,1)的抛物线的表达式13. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .
 14. 如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .
14. 如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 . 15. 对两个不相等的实数根a、b,我们规定符号 表示a、b中较大的数,如: ,按照这个规定:方程 的解为 .
15. 对两个不相等的实数根a、b,我们规定符号 表示a、b中较大的数,如: ,按照这个规定:方程 的解为 .三、解答题
-
16. 解一元二次方程:x2+4x﹣5=0.17. 如图, 的顶点坐标分别为 .
 (1)、请画出 关于点 成中心对称的 ,并写出点 的坐标;(2)、四边形 的面积为 .18. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.19. 如图,⊙O为锐角△ABC的外接圆,半径为5.(1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);(2)、若(1)中的点E到弦BC的距离为3,求弦CE的长.
(1)、请画出 关于点 成中心对称的 ,并写出点 的坐标;(2)、四边形 的面积为 .18. 已知关于 的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若 ,且该方程的两个实数根的差为2,求 的值.19. 如图,⊙O为锐角△ABC的外接圆,半径为5.(1)、用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E(保留作图痕迹,不写作法);(2)、若(1)中的点E到弦BC的距离为3,求弦CE的长. 20. 某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.(1)、请直接写出y(个)与x(元)之间的函数关系式;(2)、当销售单价是多少元时,该网店每星期的销售利润是2400元?(3)、当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?
20. 某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.(1)、请直接写出y(个)与x(元)之间的函数关系式;(2)、当销售单价是多少元时,该网店每星期的销售利润是2400元?(3)、当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?