山东省菏泽市鄄城县2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、平行四边形 B、等腰三角形 C、等边三角形 D、菱形

查看试题解析
2. 一元二次方程x²﹣2x+3＝0根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
3. 某学校组织学生到社区开展公益宣传活动，成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队，如果小华和小丽每人随机选择参加其中一个宣传队，则她们恰好选到同一个宣传队的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 4 x = 5$ 时，此方程可变形为（）

A、 ${(x + 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
5. 如图，△ACD和△ABC相似需具备的条件是（）

A、 $\frac{A C}{C D} = \frac{A B}{B C}$ B、 $\frac{C D}{A D} = \frac{B C}{A C}$ C、AC²=AD•AB D、CD²=AD•BD

查看试题解析
6. 如图所示，某同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时尺子的刻度为12cm，已知臂长60cm，则电线杆的高度为（）

A、2.4m B、24m C、0.6m D、6m

查看试题解析
7. 如图，矩形ABCD中，AC交BD于点O，∠AOD=60°，OE⊥AC．若AD= $\sqrt{3}$ ，则OE=（）

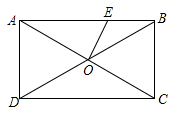A、1 B、2 C、3 D、4

查看试题解析
8. 如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（）时，△ABE与以D、M、N为顶点的三角形相似.

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{5}$ 或 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$ 或 $\frac{3 \sqrt{5}}{5}$

查看试题解析

二、填空题

9. 一元二次方程（x+1）（3x-2）=10的一般形式是.

查看试题解析
10. 如图标记了△ABC和△DEF的边，角的一些数据，请你添加一个条件，使△ABC∽△DEF，这个条件可以是．（只填一个即可）

查看试题解析
11. 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作AE⊥BD，垂足为点E，若∠EAC=2∠CAD，则∠BAE=度．

查看试题解析
12. 如图，创新广场上铺设了一种新颖的石子图案，它由五个过同一点且半径不同的圆组成，其中阴影部分铺黑色石子，其余部分铺白色石子．小鹏在规定地点随意向图案内投掷小球，每球都能落在图案内，经过多次试验，发现落在一、三、五环（阴影）内的概率分别是0.04，0.2，0.36，如果最大圆的半径是1米，那么黑色石子区域的总面积约为平方米（精确到0.01平方米）．

查看试题解析
13. 关于x的方程 $(a - 5) x^{2} - 4 x - 1 = 0$ 有实数根，则a满足．

查看试题解析
14. 如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S_△BDE：S_△CDE＝1：3，则S_△DOE：S_△AOC的值为．

查看试题解析

三、解答题

15. 解下列方程

(1)、 $x^{2} - 4 x - 3 = 0$

(2)、 ${(x - 3)}^{2} + 2 x (x - 3) = 0$

查看试题解析
16. 如图，△ABC的高AD，BE交于点F．写出图中所有与△AFE相似的三角形，并选择一个进行证明．

查看试题解析
17.
如图，在平行四边形ABCD中，∠BAD的平分线交CD于点E ，交BC的延长线于点F ，连接BE ， ∠F=45°．求证：四边形ABCD是矩形

查看试题解析
18. 某水果超市原来平均每天可销售某种水果200千克，每千克可盈利6元，为减少库存，经市场调查，如果这种水果每千克降价1元，则每天可所多售出20千克．若要平均每天盈利960元，则每千克应降价多少元？

查看试题解析
19. 如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．

(1)、画出△ABC关于x对称的△A₁B₁C₁；

(2)、以原点O为位似中心，在x轴的上方画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2，并求出△A₂B₂C₂的面积．

查看试题解析
20. 如图，△ABC中，AB=AC，∠BAC=108°，在BC边上取一点D，使BD=BA，连接AD．求证：

(1)、△ADC∽△BAC；

(2)、点D是BC的黄金分割点．

查看试题解析
21. 小明、小芳做一个“配色”的游戏．右图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，这种情况下小芳获胜；同样，蓝色和黄色在一起配成绿色，这种情况下小明获胜；在其它情况下，则小明、小芳不分胜负．

(1)、利用列表或树状图的方法表示此游戏所有可能出现的结果；

(2)、此游戏的规则，对小明、小芳公平吗？试说明理由．

查看试题解析
22. 已知关于x的方程x²﹣mx+m﹣3＝0．

(1)、若此方程的一个根为2，求另一个根及m的值

(2)、求证：不论m取何实数，方程总有两个不相等的实数根．

查看试题解析
23. 已知：如图，平行四边形ABCD中，O是CD的中点，连接AO并延长，交BC的延长线于点E．

(1)、求证： $△ A O D ≌ △ E O C$ ；

(2)、连接AC，DE，当 $∠ B = ∠ A E B =$ $°$ 四边形ACED是正方形？请说明理由．

查看试题解析
24. 从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

(1)、如图①，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40^{\circ} ， ∠ B = 60^{\circ}$ ，求证： $C D$ 是 $△ A B C$ 的完美分割线；

(2)、如图②，在 $△ A B C$ 中， $A C = 2 ， B C = \sqrt{2} ， C D$ 是 $△ A B C$ 的完美分割线，且 $△ A C D$ 是以 $C D$ 为底边的等腰三角形，求完美分割线 $C D$ 的长．

查看试题解析