辽宁省营口市大石桥市2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 关于x的方程 $(m - 3) x^{m^{2} - 2 m - 1} - m x + 6 = 0$ 是一元二次方程，则它的一次项系数是（）

A、－1 B、1 C、3 D、3或－1

查看试题解析
2. 在下列四个图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 抛物线 $y = x^{2} - 6 x + 4$ 的顶点坐标是（）

A、 $(3 ， 5)$ B、 $(- 3 ， 5)$ C、 $(3 ， - 5)$ D、 $(- 3 ， - 5)$

查看试题解析
4. 已知二次函数y=kx²-7x-7的图象和x轴有交点，则k的取值范围是（）

A、k>- $\frac{7}{4}$ B、k>- $\frac{7}{4}$ 且k≠0 C、k≥- $\frac{7}{4}$ D、k≥- $\frac{7}{4}$ 且k≠0

查看试题解析
5. 用配方法解一元二次方程 $x^{2} + 4 x - 5 = 0$ ，此方程可变形为（）

A、 ${(x + 2)}^{2} = 9$ B、 ${(x - 2)}^{2} = 9$ C、 ${(x + 2)}^{2} = 1$ D、 ${(x - 2)}^{2} = 1$

查看试题解析
6. 如图，四边形ABCD是⊙O的内接四边形，若∠A=70°，则∠C的度数是（）

A、100° B、110° C、120° D、130°

查看试题解析
7. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A、y=﹣2（x﹣1）²+2 B、y=﹣2（x﹣1）²﹣2 C、y=﹣2（x+1）²+2 D、y=﹣2（x+1）²﹣2

查看试题解析
8. 如图，△ABC以点O为旋转中心，旋转180°后得到 $△ A^{'} B^{'} C^{'}$ ．ED是△ABC的中位线，经旋转后为线段 $E^{'} D^{'}$ ．已知 $E^{'} D^{'} = 2$ ，则BC的值是（）

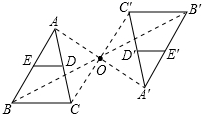A、1 B、2 C、4 D、5

查看试题解析
9. 如图，△ABC内接于⊙O，∠C＝30°，AB＝2，则⊙O的半径为（）

A、 $\sqrt{3}$ B、 $2$ C、 $2 \sqrt{3}$ D、 $4$

查看试题解析
10. 二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①a＜0，②b＞0，③b2﹣4ac＞0，④a+b+c＜0，其中结论正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若二次函数y＝（m+1）x^|m|的图象的开口向下，则m的值为．

查看试题解析
12. 点P（﹣4，6）与Q（2m，﹣6）关于原点对称，则m＝．

查看试题解析
13. 半径为5的⊙O内有一点P，且OP＝4，则过点P的最短弦长是．

查看试题解析
14. 某工厂今年一月份生产防疫护目镜的产量是20万件，计划之后两个月增加产量，如果月平均增长率为x ，那么第一季度防疫护目镜的产量y（万件）与x之间的关系应表示为．

查看试题解析
15. 已知二次函数y= $\frac{1}{2}$ （x﹣1）²+4，若y随x的增大而减小，则x的取值范围是．

查看试题解析
16. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE.若点D在线段BC的延长线上，则 $∠ B$ 的大小为.

查看试题解析

三、解答题

17. 解方程：

(1)、x²﹣2x﹣1＝0

(2)、x²﹣3x﹣2＝0

查看试题解析
18. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，建立如图所示的平面直角坐标系， $△ A B C$ 的顶点均在格点上，点 $B$ 的坐标为（1，0）．

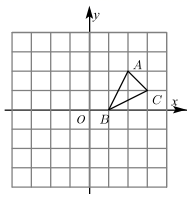(1)、画出将 $△ A B C$ 绕原点 $O$ 按顺时针旋转90°所得的 $△ A_{1} B_{1} C_{1}$ ，并写出 $C_{1}$ 点的坐标．

(2)、求线段 $C C_{1}$ 的长度．

查看试题解析
19. 已知关于x的方程 $x^{2} - 2 (m + 1) x + m^{2} = 0$

(1)、当m取何值时，方程有两个实数根；

(2)、为m选取一个合适的整数，使方程有两个不相等的实数根，并求出这两个实数根.

查看试题解析
20. 某幢建筑物，从5米高的窗口 $A$ 用水管向外喷水，喷出的水呈抛物线状（抛物线所在的平面与墙面垂直，如图所示），如果抛物线的最高点 $M$ 离墙1米，此时高度为10米．如图，在所示的平面直角坐标系中，求水流落地点 $B$ 离墙距离 $O B$ ．（结果保留根号）

查看试题解析
21. 如图是宽为20m，长为32m的矩形耕地，要修筑同样宽的三条道路（互相垂直），把耕地分成六块大小相等的试验地，要使试验地的面积为570m² ，问：道路宽为多少米？

查看试题解析
22. 如图所示，AB是⊙O的弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．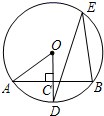

(1)、若∠AOD＝56°，求∠DEB的度数；

(2)、若DC＝2，OA＝10，求AB的长．

查看试题解析
23. 为满足市场需求，某超市在新年来临前夕，购进一款商品，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现；当售价定为每盒45元时，每天可以卖出700盒，如果每盒售价每提高1元，则每天要少卖出20盒．

(1)、试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

(2)、要使每天销售的利润为6000元，且让顾客得到最大的实惠．售价应定为多少元？

(3)、当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

查看试题解析
24. 在正方形ABCD中，M是BC边上一点，且点M不与B、C重合，点P在射线AM上，将线段AP绕点A顺时针旋转90°得到线段AQ，连接BP，DQ．

(1)、依题意补全图形，并求证：DQ＝BP

(2)、当点P在射线AM上的某一点，连接DP，若点P，Q，D恰好在同一条直线上，求证：DP²＋DQ²＝2AB²

查看试题解析
25. 如图，已知点A的坐标为（－2，0），直线y＝－ $\frac{3}{4}$ x＋3与x轴，y轴分别交于点B和点C，连接AC，顶点为D的抛物线y＝ax²＋bx＋c，过A，B，C三点．

(1)、求抛物线的解析式及顶点D的坐标；

(2)、设抛物线的对称轴DE交线段BC于点E，P为第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；

(3)、设点M是线段BC上的一动点，过点M作MN∥AB，交AC于点N．点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒）．当以MN为直角边的△QMN是等腰直角三角形时，直接写出此时t的取值．

查看试题解析