辽宁省锦州市北镇市2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 矩形具有而一般平行四边形不具有的性质是（）

A、对边平行且相等 B、对角线相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
2. 已知关于x的方程(a﹣3)x^|a^﹣^1|+x﹣1＝0是一元二次方程，则a的值是（）

A、﹣1 B、2 C、﹣1或3 D、3

查看试题解析
3. 学校组织校外实践活动，安排给九年级三辆车，小明与小红都可以从这三辆车中任选一辆搭乘，小明与小红同车的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 有下列说法：①所有的等腰三角形都相似；②所有的等边三角形都相似；③所有的正方形都相似；④所有的矩形都相似，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 用配方法解方程x²﹣2x﹣5=0时，原方程应变形为（）

A、（x+1）²=6 B、（x+2）²=9 C、（x﹣1）²=6 D、（x﹣2）²=9

查看试题解析
6. 如图，在菱形ABCD中，对角线AC，BD相交于点O，E是CD的中点，若OE＝2，则菱形ABCD的周长为（）

A、4 B、8 C、12 D、16

查看试题解析
7. 如图，直线AB//CD//EF，若BD：DF＝3：4，AC＝3.6，则AE的长为（）

A、4.8 B、6.6 C、7.6 D、8.4

查看试题解析
8. 如图，在矩形ABCD中，AB＝6cm，对角线AC＝10cm，动点P从点A出发，以2cm/s的速度沿折线AB﹣BC向终点C运动．设点P的运动时间为ts，△APC的面积为Scm² ，则下列图象能大致反映S与t之间函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 顺次连接对角线相等的四边形的四边中点，所得的四边形一定是.

查看试题解析
10. 若关于x的一元二次方程3x²﹣x+k＝0的一个根为1，则k的值为．

查看试题解析
11. 已知a，b，c，d是成比例线段，其中a＝3cm，b＝2cm，c＝6cm，则d＝cm．

查看试题解析
12. 在一个不透明的袋子中装有6个红球和若干个白球，这些球除颜色外都相同，将球搅匀后随机摸出一个球，记下颜色后放回，不断重复这一过程，共摸球100次，发现有20次摸到红球，估计袋子中白球的个数约为.

查看试题解析
13. 若关于x的一元二次方程mx²－3x＋1=0有实数根，则m的取值范围是．

查看试题解析
14. 如图，在菱形ABCD中，对角线AC，BD交于点O，其中OA＝1，OB＝2，P为BC上一动点，则AP的最小值为．

查看试题解析
15. 如图，长方形纸片ABCD中，AB＝6 cm，BC＝8 cm点E是BC边上一点，连接AE并将△AEB沿AE折叠，得到△AEB′，以C，E，B′为顶点的三角形是直角三角形时，BE的长为cm.

查看试题解析
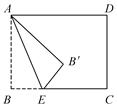16. 如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA＝OB＝1，以线段AB为边在第一象限作第一个正方形ABCD；延长CD，交x轴于点E，再以线段CE为边在第一象限作第二个正方形ECGF；延长GF，交x轴于点H，再以线段GH为边在第一象限作第三个正方形HGNM；....依此方法作下去，第n个正方形的边长是．

查看试题解析

三、解答题

17. 按指定的方法解方程：

(1)、x²﹣2 $\sqrt{3}$ x+2＝0；（公式法）

(2)、x²﹣1＝3x﹣3．（因式分解法）

查看试题解析
18. 已知 $\frac{a + b}{b} = \frac{3}{2}$ （b≠0），求 $\frac{3 a - b}{2 b}$ 的值．

查看试题解析
19. 学校计划举行“文明环保，从我做起”征文比赛．甲班的2名同学A和B与乙班的2名同学C和D在预赛中成绩优秀．

(1)、若从4名同学中选取1名同学参加学校决赛，则同学C被选中的概率是；

(2)、学校决定从4名同学中随机选取2名同学参加决赛，请用画树状图或列表的方法，求选中的2名同学恰好来自同一个班级的概率．

查看试题解析
20. 如图，△ABC中，DE∥BC，EF∥AB，AE＝2CE，AB＝12，BC＝18，求四边形BDEF的周长．

查看试题解析
21. 某县为发展教育事业，从2019年开始加强了对教育经费的投入.2019年投入的教育经费为1000万元，计划以后每年以相同的增长率投入，2021年投入的教育经费达到1440万元．

(1)、求该县投入教育经费的年平均增长率；

(2)、若投入教育经费的年平均增长率继续保持不变，预计2022年该县将投入教育经费多少万元？

查看试题解析
22. 某商场销售一批运动衫，已知该运动衫的进价为每件40元，当售价为每件60元时，每个月可售出100件．根据市场行情，现决定涨价销售，调查表明，每件商品的售价每上涨1元，每个月会少售出2件，设每件商品的售价为x元，每个月的销量为y件．

(1)、求y与x之间的函数关系式；

(2)、当每件商品的售价定为多少元时，每个月的利润恰好为2250元．

查看试题解析
23. 如图，在正方形ABCD中，点E，F分别在AD，CD上，且AE＝DF，BE与AF相交于点O，P是BF的中点，连接OP．

(1)、试判断AF与BE的关系，并证明你的结论；

(2)、若AB＝5，AE＝2，求OP的长．

查看试题解析
24. 四边形ABCD是菱形，∠ABC＝60°，E是对角线BD上的一个动点，连接AE，将线段AE绕点A逆时针旋转120°得到线段AF，连接EF，DF．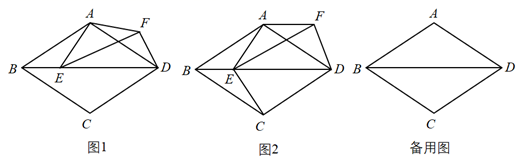

(1)、如图1，求∠BDF的度数；

(2)、如图2，当DB＝3DF时，连接EC，求证：四边形FECD是矩形；

(3)、若G为DF中点，连接EG，当线段BD与DF满足怎样的数量关系时，四边形AEGF是菱形，并说明理由．

查看试题解析