辽宁省葫芦岛市连山区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 若关于 的一元二次方程 的常数项为 ,则 的值等于( )A、2 B、−2 C、±2 D、−42. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、 B、 ,且 C、 ,且 D、3. 下列图形,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、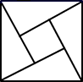 D、
D、 4. 一次函数 的图象如图所示,则二次函数 的图象可能是( )
4. 一次函数 的图象如图所示,则二次函数 的图象可能是( ) A、
A、 B、
B、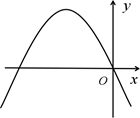 C、
C、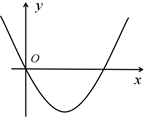 D、
D、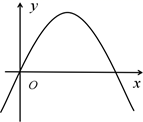 5. 已知二次函数 的图象交 轴于 两点.若其图象上有且只有 三点满足 ,则 的值是( )A、1 B、 C、2 D、46. 如图,将 绕点A逆时针旋转 得到 ,若 且 于点F,则 的度数为( )
5. 已知二次函数 的图象交 轴于 两点.若其图象上有且只有 三点满足 ,则 的值是( )A、1 B、 C、2 D、46. 如图,将 绕点A逆时针旋转 得到 ,若 且 于点F,则 的度数为( ) A、 B、 C、 D、7. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )
A、 B、 C、 D、7. 往直径为 的圆柱形容器内装入一些水以后,截面如图所示,若水面宽 ,则水的最大深度为( )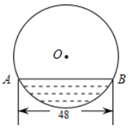 A、 B、 C、 D、8. 如图,A,B,C是半径为1的⊙O上的三个点,若AB= ,∠CAB=30°,则∠ABC的度数为( )
A、 B、 C、 D、8. 如图,A,B,C是半径为1的⊙O上的三个点,若AB= ,∠CAB=30°,则∠ABC的度数为( ) A、95° B、100° C、105° D、110°9. 如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A、95° B、100° C、105° D、110°9. 如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )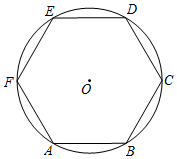 A、60° B、60°或120° C、30° D、30°或150°10. 如图,平行四边形纸片ABCD,CD=5,BC=2,∠A=60°,将纸片折叠,使点A落在射线AD上(记为点A′),折痕与AB交于点P,设AP的长为x,折叠后纸片重叠部分的面积为y,可以表示y与x之间关系的大致图象是( )
A、60° B、60°或120° C、30° D、30°或150°10. 如图,平行四边形纸片ABCD,CD=5,BC=2,∠A=60°,将纸片折叠,使点A落在射线AD上(记为点A′),折痕与AB交于点P,设AP的长为x,折叠后纸片重叠部分的面积为y,可以表示y与x之间关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知关于x的一元二次方程 的一个解是 ,则 .12. 已知二次函数 的图象的顶点在x轴上方,则实数k的取值范围是 .13. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.14. 如图,在平面直角坐标系中,平行四边形 的顶点A、B在x轴上,顶点D在y轴上,点A的坐标为 ,点C的坐标为 .一条直线经过点 .且将平行四边形 分割成面积相等的两部分,则此直线的表达式是 .
 15. 如图,四边形 是 的内接四边形, ,弦 ,则 的半径等于 .
15. 如图,四边形 是 的内接四边形, ,弦 ,则 的半径等于 . 16. 将半径为 的扇形围成一个圆锥的侧面,若扇形的圆心角是 ,则该圆锥底面的半径为 .17. 如图,在 中, ,边 上有一动点P,将 绕点C逆时针旋转 得 ,点P的对应点为 ,连接 ,则 长的最小值为 .
16. 将半径为 的扇形围成一个圆锥的侧面,若扇形的圆心角是 ,则该圆锥底面的半径为 .17. 如图,在 中, ,边 上有一动点P,将 绕点C逆时针旋转 得 ,点P的对应点为 ,连接 ,则 长的最小值为 . 18. 如图,P是正方形 内一点, ,将线段 以点A为旋转中心逆时针旋转 得到线段 ,连接 下列结论:
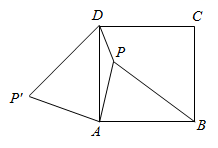
18. 如图,P是正方形 内一点, ,将线段 以点A为旋转中心逆时针旋转 得到线段 ,连接 下列结论:① 可以由 绕点A逆时针旋转 得到;②点P与 的距离为2;③ ;④ ;⑤ .其中正确的结论是(填序号).
三、解答题
-
19. 解方程:(1)、 .(2)、20. 在下面的网格中,每个小正方形的边长均为1, 的三个顶点都是网格线的交点,已知B,C两点的坐标分别为 .
 (1)、请在图中画出平面直角坐标系,并直接写出点A的坐标;(2)、将 绕着坐标原点顺时针旋转 ,画出旋转后的 ;(3)、设 为 边上一点,在 上与点P对应的点是 ,则点 坐标为;(4)、在上述旋转过程中,点A所经过的路径长为 .21. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.22. 如图,在平行四边形 中, ,以 为直径的 与 相切于点E,连接 ,若 .
(1)、请在图中画出平面直角坐标系,并直接写出点A的坐标;(2)、将 绕着坐标原点顺时针旋转 ,画出旋转后的 ;(3)、设 为 边上一点,在 上与点P对应的点是 ,则点 坐标为;(4)、在上述旋转过程中,点A所经过的路径长为 .21. “杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水箱亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.(1)、如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;(2)、按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,请通过计算说明他们的目标能否实现.22. 如图,在平行四边形 中, ,以 为直径的 与 相切于点E,连接 ,若 .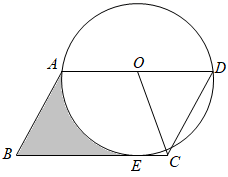 (1)、求 的长度?(2)、求线段 与弧 围成的图形(阴影部分)的面积?23. 如图,等边三角形 ,点O在 上,以点O为圆心, 为半径作 ,交 于点D,作 于点E,连接 .
(1)、求 的长度?(2)、求线段 与弧 围成的图形(阴影部分)的面积?23. 如图,等边三角形 ,点O在 上,以点O为圆心, 为半径作 ,交 于点D,作 于点E,连接 . (1)、求证: 是 的切线;(2)、若 的半径 ,且 时,求 的长度.24. 某服装厂生产A品种服装,每件成本为67元,向外批发时,要求批发件数x为10的正整数倍,且 ;零售商到此服装厂一次性批发A品牌服装,批发单价为y元,y与x之间满足如图所示的函数关系.
(1)、求证: 是 的切线;(2)、若 的半径 ,且 时,求 的长度.24. 某服装厂生产A品种服装,每件成本为67元,向外批发时,要求批发件数x为10的正整数倍,且 ;零售商到此服装厂一次性批发A品牌服装,批发单价为y元,y与x之间满足如图所示的函数关系. (1)、求y与x的函数关系式;(2)、零售商到此服装一次性批发A品牌服 件,服装厂的利润为w元,问x为何值时,w最大?最大值是多少?(3)、零售商到此服装厂一次性批发A品牌服装件数x在什么范围时?可使服装厂获利不低于4420元,请直接写出结果.25. 如图,在 和 中, , , ,连接 ,点H为 的中点,连接 , ,将 绕点A旋转.
(1)、求y与x的函数关系式;(2)、零售商到此服装一次性批发A品牌服 件,服装厂的利润为w元,问x为何值时,w最大?最大值是多少?(3)、零售商到此服装厂一次性批发A品牌服装件数x在什么范围时?可使服装厂获利不低于4420元,请直接写出结果.25. 如图,在 和 中, , , ,连接 ,点H为 的中点,连接 , ,将 绕点A旋转. (1)、如图1,当点D在 延长线上时,直接写出线段 和 之间的数量关系为 . 位置关系为 .(2)、如图2,当点D旋转到 延长线上时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、若 , ,当 时,请直接写出线段 的长.26. 如图,在半面直角坐标系中,抛物线 与x轴交于点A、B,其中点A的坐标为 ,与y轴交于点 .
(1)、如图1,当点D在 延长线上时,直接写出线段 和 之间的数量关系为 . 位置关系为 .(2)、如图2,当点D旋转到 延长线上时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、若 , ,当 时,请直接写出线段 的长.26. 如图,在半面直角坐标系中,抛物线 与x轴交于点A、B,其中点A的坐标为 ,与y轴交于点 . (1)、求抛物线的解析式;(2)、若点D为抛物线上 上方的一个动点,过点D作 轴,交 于点E,过D作 ,交直线 于点F,以 、 为边作矩形 ,设矩形 的周长为l,求l的最大值;(3)、点P是x轴上一动点,将线段 绕点P旋转 得到 ,当点Q刚好落在抛物线上时,请直接写出点Q的坐标.
(1)、求抛物线的解析式;(2)、若点D为抛物线上 上方的一个动点,过点D作 轴,交 于点E,过D作 ,交直线 于点F,以 、 为边作矩形 ,设矩形 的周长为l,求l的最大值;(3)、点P是x轴上一动点,将线段 绕点P旋转 得到 ,当点Q刚好落在抛物线上时,请直接写出点Q的坐标.