辽宁省鞍山市岫岩满族自治县2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是一元二次方程的是（）

A、 $x y + 2 = 1$ B、 $x^{2} + \frac{1}{2 x} - 9 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $x^{2} = 0$

查看试题解析
2. 下列图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，已知AB∥CD∥EF且AC∶CE＝3∶4，BF＝14，则DF的长为（）

A、8 B、7 C、6 D、3

查看试题解析
4. 已知二次函数 $y = 2 x^{2} + 8 x + 7$ 的图象上有点 $A (- 2 ， y_{1})$ ， $B (- 5 ， y_{2})$ ， $C (- 1 ， y_{3})$ ，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{2} > y_{3} > y_{1}$ D、 $y_{3} > y_{1} > y_{1}$

查看试题解析
5. 如图，△ABC与△BEF位似，点O是它们的位似中心，其中OE=2OB，则△ABC与△DEF的周长之比是（）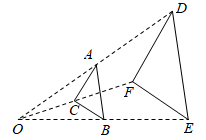

A、1：2 B、1：4 C、1：3 D、1：9

查看试题解析
6. 现要在一个长为 $40 m$ ，宽为 $26 m$ 的矩形花园中修建等宽的小道，剩余的地方种植花草，如图所示，要使种植花草的面积为 $950 m^{2}$ ，那么小道的宽度应是（）

A、 $1 m$ B、 $1.5 m$ C、 $2 m$ D、 $2.5 m$

查看试题解析
7. 如图，在平面直角坐标系中，线段 $O A$ 与 $x$ 轴正方向夹角为 $45 °$ ，且 $O A = 2$ ，若将线段 $O A$ 绕点 $O$ 沿逆时针方向旋转 $105 °$ 到线段 $O A^{'}$ ，则此时点 $A^{'}$ 的坐标为（）

A、 $(\sqrt{3} ， - 1)$ B、 $(- 1 ， \sqrt{3})$ C、 $(- \sqrt{3} ， 1)$ D、 $(1 ， - \sqrt{3})$

查看试题解析
8. 如图， $Rt △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， $A B = 20$ ，点 $P$ 是 $A C$ 边上的一个动点，将线段 $B P$ 绕点 $B$ 顺时针旋转 $60 °$ 得到线段 $B Q$ ，连接 $C Q$ ，则在点 $P$ 运动过程中，线段 $C Q$ 的最小值为（）

A、 $5$ B、 $10$ C、 $20$ D、 $25$

查看试题解析

二、填空题

9. 若y＝（m﹣4）x^|m|^﹣2﹣2x﹣1是关于x的二次函数，则m＝．

查看试题解析
10. 已知0是关于 $x$ 的一元二次方程 $(m - 1) x^{2} + x + m^{2} - 1 = 0$ 的一个根，则 $m$ 的值是．

查看试题解析
11. 把抛物线 $y = 3 x^{2}$ 先向上平移2个单位，再向右平移3个单位，所得抛物线的解析式为

查看试题解析
12. 如图，小明为了测量高楼 $M N$ 的高度，在离点 $N 18$ 米的点 $A$ 处放了一个平面镜，小明沿 $N A$ 方向后退 $1.5$ 米到点 $C$ ，此时从镜子中恰好看到楼顶的点 $M$ ，已知小明的眼睛（点 $B$ ）到地面的高度 $B C$ 是 $1.6$ 米，则高楼 $M N$ 的高度是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ B A C = 108 °$ ，将 $△ A B C$ 绕点 $A$ 按逆时针方向旋转得到 $△ A B^{'} C^{'}$ ．若点 $B^{'}$ 恰好落在 $B C$ 边上，且 $A B^{'} = C B^{'}$ ，则 $∠ C^{'}$ 的度数为．

查看试题解析
14. 如图，点 $A$ 在数轴的负半轴，点 $B$ 在数轴的正半轴，且点 $A$ 对应的数是 $2 x - 1$ ，点 $B$ 对应的数是 $x^{2} + x$ ，已知 $A B = 5$ ，则 $x$ 的值为．

查看试题解析
15. 将二次函数y＝x²﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y＝2x+b与这个新图象有3个公共点，则b的值为．

查看试题解析
16. 如图，在平面直角坐标系中，正方形 $A B C D$ 的顶点 $A$ 的坐标为 $(\frac{\sqrt{5}}{5} ， 0)$ ，顶点 $D$ 的坐标为 $(0 ， \frac{2}{5} \sqrt{5})$ ，延长 $C B$ 交 $x$ 轴于点 $A_{1}$ ．作正方形 $A_{1} B_{1} C_{1} C$ ，延长 $C_{1} B_{1}$ 交 $x$ 轴于点 $A_{2}$ ，作正方形 $A_{2} B_{2} C_{2} C_{1}$ ，……，按这样的规律进行下去，第 $2021$ 个正方形的边长为．

查看试题解析

三、解答题

17. 解方程：

(1)、 $5 x^{2} - 3 x = x + 1$

(2)、 $3 x (2 x + 1) = 4 x + 2$

查看试题解析
18. 如图，在平面直角坐标系中，已知 $△ A B C$ 三个顶点的坐标分别为 $A (- 1 ， 2) ， B (- 3 ， 4) ， C (- 2 ， 6)$ ．

（ 1 ）画出 $△ A B C$ 绕点A顺时针旋转 $90 °$ 后得到的 $△ A_{1} B_{1} C_{1}$ ，写出点 $C_{1}$ 的坐标．

（ 2 ）以原点O为位似中心，在网格内画出将 $△ A_{1} B_{1} C_{1}$ 三条边放大为原来的2倍后得 $△ A_{2} B_{2} C_{2}$ ，写出点 $B_{2}$ 的坐标．

查看试题解析
19. 已知关于 $x$ 的方程 $x^{2} - (m + 1) x + 2 (m - 1) = 0$

(1)、求证：无论 $m$ 取何值时，方程总有实数根；

(2)、若等腰三角形一边长为 $4$ ，另两边恰好是此方程的根，求此三角形的另两边长．

查看试题解析
20. 近日，长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意见》鼓励教师与志愿辅导，某区率先示范，推出名师公益大课堂，为学生提供线上线下免费辅导，据统计，第一批公益课受益学生2万人次，第三批公益课受益学生2.42万人次．

(1)、如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率；

(2)、按照这个增长率，预计第四批公益课受益学生将达到多少万人次？

查看试题解析
21. 如图，在 $△ A B C$ 中， $P C$ 平分 $∠ A C B$ ， $P B = P C$ ．

(1)、求证： $△ A P C \sim △ A C B$ ；

(2)、若 $A P = 2$ ， $P C = 5$ ，求 $A C$ 的长．

查看试题解析
22. 如图所示，一个运动员推铅球，铅球在点 $A$ 处出手，出手时球离地面约 $\frac{5}{3}$ 米，铅球落地点在 $B$ 处，铅球运行中在运动员前 $4$ 米处（即 $O C = 4$ ）达到最高点，最高点高为 $3$ 米，已知铅球经过的路线是抛物线．根据图示的直角坐标系回答下列问题．

(1)、求铅球所经过路线的函数表达式．

(2)、铅球的落地点离运动员有多远?

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以5cm/s的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以4cm/s的速度向点B匀速运动，运动时间为t s（0＜t＜2），连接PQ．

(1)、若△BPQ和△ABC相似，求t的值；

(2)、连接AQ，CP，若AQ⊥CP，求t的值．

查看试题解析
24. 小明在淘宝上销售一批口罩．经市场调研：某类型口罩进价每袋为 $20$ 元，当售价为每袋 $25$ 元时，销售量为 $250$ 袋，若销售单价每提高 $1$ 元，销售量就会减少 $10$ 袋．

(1)、直接写出小明销售该类型口罩销售量 $y$ （袋）与销售单价 $x$ （元）之间的函数关系式；每天所得销售利润 $w$ （元）与销售单价 $x$ （元）之间的函数关系式．

(2)、若每天销售量不少于 $100$ 袋，且每袋口罩的销售利润至少为 $17$ 元，则销售单价定为多少元时，此时利润最大，最大利润是多少?

查看试题解析
25. 在 $△ A B C$ 中， $C A = C B$ ， $∠ A C B = α$ ，点 $P$ 是平面内不与点 $A$ 、 $C$ 重合的任意一点，连接 $A P$ ，将线段 $A P$ 绕点 $P$ 逆时针旋转 $α$ 得到线段 $D P$ ，连接 $A D$ 、 $B D$ 、 $C P$ ．

(1)、如图（1），当 $α = 60 °$ 时， $\frac{B D}{C P}$ 的值是，直线 $B D$ 与直线 $C P$ 相交所成的较小角的度数是．

(2)、如图（2），当 $α = 90 °$ 时，请求出 $\frac{B D}{C P}$ 的值及直线 $B D$ 与直线 $C P$ 相交所成的较小角的度数．

(3)、如图（3），当 $α = 90 °$ 时，若点 $E$ 、 $F$ 分别是 $C A$ 、 $C B$ 的中点，点 $P$ 在直线 $E F$ 上，请直接写出当点 $C$ 、 $P$ 、 $D$ 在同一直线上时 $\frac{A D}{C P}$ 的值．

查看试题解析
26. 如图，抛物线 $L ： y = a x^{2} + b x + 3$ 与 $x$ 轴交于 $A$ 、 $B (3 ， 0)$ 两点（ $A$ 在 $B$ 的左侧），与 $x$ 轴交于 $A$ 、 $B$ 两点，且点 $B$ 坐标为 $(3 ， 0)$ 与 $y$ 轴交于点 $C$ ，已知对称轴 $x = 1$ ．

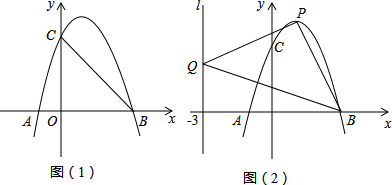(1)、求抛物线 $L$ 的解析式；

(2)、将抛物线 $L$ 向下平移 $h$ 个单位长度，使平移后所得抛物线的顶点落在 $△ O B C$ 内（包括 $△ O B C$ 的边界），求 $h$ 的取值范围：

(3)、设点 $P$ 是抛物线 $L$ 上任一点，点 $Q$ 在直线 $l ： x = - 3$ 上， $△ P B Q$ 能否成为以点 $P$ 为直角顶点的等腰直角三角形?若能，求出符合条件的点 $P$ 的坐标：若不能，请说明理由．

查看试题解析