吉林省吉林市永吉县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 一元二次方程3x2﹣x﹣2=0的二次项系数、一次项系数、常数项分别是( )A、3,﹣1,﹣2 B、3,1,﹣2 C、3,﹣1,2 D、3,1,22. 下面四幅球类的平面图案中,是中心对称图形的是( )A、
 B、
B、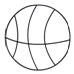 C、
C、 D、
D、 3. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、4. 抛物线 经过平移得到 ,则这个平移过程正确的是( )A、向左平移1个单位 B、向右平移1个单位 C、向上平移1个单位 D、向下平移1个单位5. 如图,小林坐在秋千上,秋千旋转了80°,小林的位置也从A点运动到了A'点,则∠OAA'的度数为( )
3. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、4. 抛物线 经过平移得到 ,则这个平移过程正确的是( )A、向左平移1个单位 B、向右平移1个单位 C、向上平移1个单位 D、向下平移1个单位5. 如图,小林坐在秋千上,秋千旋转了80°,小林的位置也从A点运动到了A'点,则∠OAA'的度数为( ) A、40° B、50° C、70° D、80°6. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( )
A、40° B、50° C、70° D、80°6. 如图,四边形 内接于 ,点 为边 上任意一点(点 不与点 , 重合)连接 .若 ,则 的度数可能为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
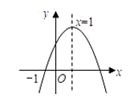
7. 已知点 与点 关于原点对称,则 的值为 .8. 若关于 的一元二次方程 有两个相等的实数根,则 的值为 .9. 某件商品原价 元,经过两次降价(每次降价的百分数相同)后,现价 元,每次降价的百分数为 则可列方程为 .10. 已知二次函数 的图象如图所示,则点 在第象限.
 11. 如图, 是 的直径,点 在 上,并且 于 若 ,则 的长为
11. 如图, 是 的直径,点 在 上,并且 于 若 ,则 的长为 12. 如图,AB是⊙O的直径,点C和点D在⊙O上,若∠BDC=20°,则∠AOC等于度.
12. 如图,AB是⊙O的直径,点C和点D在⊙O上,若∠BDC=20°,则∠AOC等于度. 13. 如图,直线 是 的切线, 为切点, 为直线 上一点,连接 交 于点 .若 ,则 的长为 .
13. 如图,直线 是 的切线, 为切点, 为直线 上一点,连接 交 于点 .若 ,则 的长为 . 14. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
14. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
三、解答题
-
15. 解方程: .16. 如图,弧 弧 求证: .
 17. 求抛物线 的顶点坐标,并直接写出 随 增大而增大时自变量 的取值范围.18. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 .如果要使彩条所占面积是图案面积的 ,应如何设计彩条的宽度?
17. 求抛物线 的顶点坐标,并直接写出 随 增大而增大时自变量 的取值范围.18. 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 .如果要使彩条所占面积是图案面积的 ,应如何设计彩条的宽度? 19. 如图,在半径为 的 中,弦 长 .求:
19. 如图,在半径为 的 中,弦 长 .求: (1)、 的度数;(2)、点O到 的距离.20. 如图是 的边长为 的正方形网格,请你在所给的网格中按下列要求操作:
(1)、 的度数;(2)、点O到 的距离.20. 如图是 的边长为 的正方形网格,请你在所给的网格中按下列要求操作:
( 1 )请在网格中建立适当的平面直角坐标系,使 点坐标为 点坐标为 点坐标为 ,并画出 ;
( 2 )画出 以点 为旋转中心,旋转 后的 (点 的对应点为 );
( 3 )写出坐标点 的坐标;
21. 如图,在 中, ,将 绕点A逆时针旋转得到 ,连接 ,使 . (1)、求 的度数;(2)、 的度数为 .22. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 .求:
(1)、求 的度数;(2)、 的度数为 .22. 如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 .求: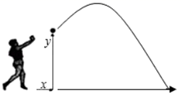 (1)、铅球在行进中的最大高度;(2)、该男生将铅球推出的距离是多少m?23. 如图, 内接于 和 相交于点 ,点 在 的延长线上,且 .
(1)、铅球在行进中的最大高度;(2)、该男生将铅球推出的距离是多少m?23. 如图, 内接于 和 相交于点 ,点 在 的延长线上,且 . (1)、试判断直线 与 的位置关系,并说明理由;(2)、若 的半径为 ,则 , 的周长为 .24. 如图,在等边 中,点 是 边上一点,连接 将 绕点 顺时针旋转 后得到 ,连接 .
(1)、试判断直线 与 的位置关系,并说明理由;(2)、若 的半径为 ,则 , 的周长为 .24. 如图,在等边 中,点 是 边上一点,连接 将 绕点 顺时针旋转 后得到 ,连接 .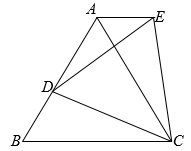 (1)、 是三角形;(2)、若 ,求 的周长;(3)、求证: .25. 某商品现在的售价为每件 元,每星期可卖出 件.市场调查反映:每降价 元,每星期可多卖出 件.已知商品的进价为每件 元,若该商品每件降价 元.(1)、该商品每星期可卖出件(用含 的代数式表示);(2)、销售该商品要想每星期盈利6120元,每件商品应降价多少元?(3)、若销售该商品每星期盈利 元,求 的最大值.26. 如图,已知二次函数图象的顶点坐标为C(1,0),直线 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴
(1)、 是三角形;(2)、若 ,求 的周长;(3)、求证: .25. 某商品现在的售价为每件 元,每星期可卖出 件.市场调查反映:每降价 元,每星期可多卖出 件.已知商品的进价为每件 元,若该商品每件降价 元.(1)、该商品每星期可卖出件(用含 的代数式表示);(2)、销售该商品要想每星期盈利6120元,每件商品应降价多少元?(3)、若销售该商品每星期盈利 元,求 的最大值.26. 如图,已知二次函数图象的顶点坐标为C(1,0),直线 与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴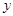 上.
上.  (1)、求m的值及这个二次函数的关系式;(2)、P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;(3)、D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
(1)、求m的值及这个二次函数的关系式;(2)、P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E点,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;(3)、D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.