广东省韶关市新丰县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-12-22 类型:期中考试
一、单选题
-
1. 下面四个图形分别是欧宝、大众、奔驰、本田四款车标志,在这四个标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中一定是关于x的一元二次方程的是( )A、ax2+bx+c = 0 B、 C、3(x+1)2 = 2(x +1) D、x2- x(x +3)= 03. 国旗上的五角星需要旋转多少度后才能与自身重合?( )A、36° B、60° C、45° D、72°4. 点(-1,2)关于原点的对称点坐标是( )A、(-1,-2) B、(1,2) C、(1,-2) D、(2,-1)5. 关于二次函数y = (x-3) 2 +5的图象,下列说法正确的是( )A、开口向下 B、顶点坐标(3,5) C、对称轴x = -3 D、有最大值56. 关于x的一元二次方程 没有实数根,则m的取值范围是( )A、m<5 B、m>-5 C、m>5 D、m<-57. 有支球队参加篮球比赛,共比赛66场,每两队之间都比赛一场,则下列方程中正确的是( )A、 x(x-1)=66 B、 x(x+1)=66 C、x(x-1)=66 D、x(x+1)=668. 三角形的两边长分别是3和6,第三边的长是方程x2-7x +10 = 0的一个根,则这个三角形的周长是( )A、11或14 B、14或16 C、14 D、119. 二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )
2. 下列方程中一定是关于x的一元二次方程的是( )A、ax2+bx+c = 0 B、 C、3(x+1)2 = 2(x +1) D、x2- x(x +3)= 03. 国旗上的五角星需要旋转多少度后才能与自身重合?( )A、36° B、60° C、45° D、72°4. 点(-1,2)关于原点的对称点坐标是( )A、(-1,-2) B、(1,2) C、(1,-2) D、(2,-1)5. 关于二次函数y = (x-3) 2 +5的图象,下列说法正确的是( )A、开口向下 B、顶点坐标(3,5) C、对称轴x = -3 D、有最大值56. 关于x的一元二次方程 没有实数根,则m的取值范围是( )A、m<5 B、m>-5 C、m>5 D、m<-57. 有支球队参加篮球比赛,共比赛66场,每两队之间都比赛一场,则下列方程中正确的是( )A、 x(x-1)=66 B、 x(x+1)=66 C、x(x-1)=66 D、x(x+1)=668. 三角形的两边长分别是3和6,第三边的长是方程x2-7x +10 = 0的一个根,则这个三角形的周长是( )A、11或14 B、14或16 C、14 D、119. 二次函数y = x2-2x-3的图象如图所示,则函数值y<0时,x的取值范围是( )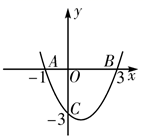 A、-1<x<3 B、x<-1 C、x>3 D、x<-1或 x>310. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
A、-1<x<3 B、x<-1 C、x>3 D、x<-1或 x>310. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )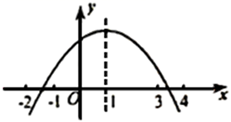 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 一元二次方程 的解是 .12. 已知y=(k-2)x|k|+2x-3是二次函数,则实数k=13. 把二次函数y = -2x 2的图象向右平移1个单位,再向上平移2个单位后得到一个新图象,则新图象所表示的二次函数的解析式是14. 已知关于x的方程 的一个根为2,则这个方程的另一个根是 .15. 二次函数y = x2+x-12与x轴的交点坐标分别是16. 如图,在宽为18m,长为36m的矩形耕地上修建同样宽的三条道路(横向与纵向垂直),把耕地分成若干小矩形块,作为小麦试验田国,假设试验田面积为450m2 , 求道路宽为多少?设宽为xm,列出的方程是
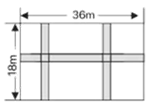 17. 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是cm.
17. 如图,在△ABC中,∠C=90°,AC=2cm,AB=3cm,将△ABC绕点B顺时针旋转60°得到△FBE,则点E与点C之间的距离是cm.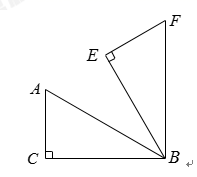
三、解答题
-
18. 解方程:19. 求二次函数 图象的顶点坐标和对称轴.20. 如图,在边长为1的小正方形格中,△AOB的顶点均在格点上,
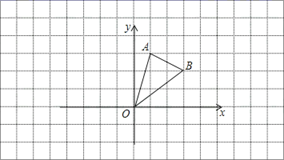 (1)、B点关于y轴的对称点坐标为;(2)、以原点O为对称中心,画出△ AOB与关于原点对称的△A1O1B1 .21. 某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)、若两次下调的百分率相同,求平均每次下调的百分率;(2)、根据(1)所得的下调的百分率,预计第三次该楼盘售价将下调到每平方米多少元?22. 已知关于x的一元二次方程 .(1)、如果此方程有两个相等的实数根,求n的值;(2)、如果此方程有一个实数根为0,求另外一个实数根.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利50元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天要赢利1600元,每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场平均每天赢利最多?24. 阅读材料:为解方程 ,我们可以将 看作一个整体,设 ①,那么原方程可化为 ,解得 , ,当 时, , , ;当 时, , , ,故原方程的解为 , , , .
(1)、B点关于y轴的对称点坐标为;(2)、以原点O为对称中心,画出△ AOB与关于原点对称的△A1O1B1 .21. 某楼盘准备以每平方米5000元的均价对外销售,由于有关部门关于房地产的新政策出台后,部分购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)、若两次下调的百分率相同,求平均每次下调的百分率;(2)、根据(1)所得的下调的百分率,预计第三次该楼盘售价将下调到每平方米多少元?22. 已知关于x的一元二次方程 .(1)、如果此方程有两个相等的实数根,求n的值;(2)、如果此方程有一个实数根为0,求另外一个实数根.23. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利50元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天要赢利1600元,每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场平均每天赢利最多?24. 阅读材料:为解方程 ,我们可以将 看作一个整体,设 ①,那么原方程可化为 ,解得 , ,当 时, , , ;当 时, , , ,故原方程的解为 , , , .以上解题方法叫做换元法,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,体现了转化的数学思想;请利用以上知识解方程:
(1)、 .(2)、 .25. 如图,已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上,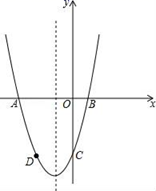 (1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点M(点C除外),使△ABM的面积等于△ABC的面积,求M点坐标.
(1)、求抛物线的表达式;(2)、抛物线的对称轴上有一动点P,求出PA+PD的最小值;(3)、若抛物线上有一动点M(点C除外),使△ABM的面积等于△ABC的面积,求M点坐标.