广东省茂名市高州市2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 若a为方程 $x^{2} + x - 5 = 0$ 的解，则 $a^{2} + a + 1$ 的值为（）

A、12 B、6 C、9 D、16

查看试题解析
2. 下列说法中，错误的是（）

A、等边三角形都相似 B、等腰直角三角形都相似 C、矩形都相似 D、正方形都相似

查看试题解析
3. 将方程 $x^{2} - 2 x - 3 = 0 化为 {(x - m)}^{2} = n$ 的形式，指出 $m ， n$ 分别是（）

A、1和3 B、-1和3 C、1和4 D、-1和4

查看试题解析
4. 下面性质中菱形有而矩形没有的是（　　）

A、邻角互补 B、内角和为360° C、对角线相等 D、对角线互相垂直

查看试题解析
5. 一个口袋中装有 4个白球，1个红球，7个黄球，搅匀后随机从袋中摸出 1个球是白球的概率是（）．

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
6. 如图，在△ABC中，点D、E分别是AB、AC的中点，则下列结论：①BC=2DE；②△ADE∽△ABC；③ $\frac{A D}{A E} = \frac{A B}{A C}$ .其中正确的有（）

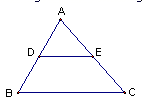A、1个 B、2个 C、3个 D、0个

查看试题解析
7. 若关于x的方程 $4 x^{2} + (m - 3) x + 1 = 0$ 有两个相等的实数根，则m值为（）

A、7 B、7或 $- 1$ C、 $- 1$ D、 $- 7$ 或1

查看试题解析
8. 下面四组线段中，不能成比例的是（）．

A、a＝3，b＝6，c＝2，d＝4 B、a＝1，b＝ $\sqrt{2}$ ，c＝ $\sqrt{6}$ ，d＝ $\sqrt{3}$ C、a＝4，b＝4，c＝5，d＝10 D、a＝2，b＝ $\sqrt{5}$ ，c＝ $\sqrt{15}$ ，d＝2 $\sqrt{3}$

查看试题解析
9. 如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么指针同时落在偶数的概率是（）

A、 $\frac{5}{25}$ B、 $\frac{6}{25}$ C、 $\frac{10}{25}$ D、 $\frac{19}{25}$

查看试题解析
10. 一个矩形的两条对角线的一个夹角为 $60 °$ ，对角线长为 $16 cm$ ，则这个矩形较短边的长为（）

A、 $2 cm$ B、 $4 cm$ C、 $8 cm$ D、 $16 cm$

查看试题解析

二、填空题

11. 如果 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ ，相似比为3∶2，若它们的周长的差为40厘米，则 $△ A^{'} B^{'} C^{'}$ 的周长为厘米．

查看试题解析
12. 关于x的一元二次方程kx²+2x-3=0有实数根，则k的取值范围是.

查看试题解析
13. 如图，∠1=∠2，添加一个条件使得△ADE∽△ACB ．

查看试题解析
14. 在一个不透明的口袋中有颜色不同的红、白两种小球，其中红球3只，白球n只，若从袋中任取一个球，摸出白球的概率为 $\frac{3}{4}$ ，则n= ．

查看试题解析
15. 如图，A、B两点被池塘隔开，在AB外取一点C，连接AC、BC，在AC上取点M，使AM=3MC，作MN∥AB交BC于N，量得MN=38m，则AB的长为．

查看试题解析

三、解答题

16. 在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请你在4×4的方格纸中，画一个格点三角形A₁B₁C₁ ，使△A₁B₁C₁与格点三角形ABC相似（相似比不为1）．

查看试题解析
17. 解方程： $x^{2} + 8 x - 20 = 0$ ．

查看试题解析
18. 如图，四边形 $A B C D$ 是边长为 $13cm$ 的菱形，其中对角线 $B D$ 长 $10cm$ ．求：

(1)、对角线 $A C$ 的长度；

(2)、菱形 $A B C D$ 的面积．

查看试题解析
19. 已知 $\frac{x}{3} = \frac{y}{5} = \frac{z}{6}$ ，且3y=2z+6，求x，y的值．

查看试题解析
20. 在一个布口袋中装有只有颜色不同，其它都相同的白、红、黑三种颜色的小球各1只，甲乙两人进行摸球游戏；甲先从袋中摸出一球看清颜色后放回，再由乙从袋中摸出一球．

(1)、试用树状图（或列表法）表示摸球游戏所有可能的结果；

(2)、如果规定：乙摸到与甲相同颜色的球为乙胜，否则为负，试求乙在游戏中能获胜的概率．

查看试题解析
21. 王老汉为了与顾客签订购销合同，对自己鱼塘中鱼的总质量进行了估计，第一次捞出100条，称得质量为184千克.并将每条鱼做上记号后放入水中，当它们完全混合于鱼群后，又捞出200条，称得质量为416千克，且带有记号的鱼有20条，王老汉的鱼塘中估计有鱼多少条鱼？总质量为多少千克？

查看试题解析
22. 商场某种商品平均每天可销售30件，每件盈利50元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多售出2件．设每件商品降价x元．据此规律，请回答：

(1)、商场日销售量增加件，每件商品盈利元（用含x的代数式表示）；

(2)、在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？

查看试题解析
23. 如图，已知平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点O， $△ A O B$ 是等边三角形， $A B = 4 cm$ ．

(1)、求证：平行四边形 $A B C D$ 是矩形；

(2)、求平行四边形 $A B C D$ 的面积．

查看试题解析
24. 已知关于x的方程 $a^{2} x^{2} + (2 a - 1) x + 1 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ．

(1)、求a的取值范围；

(2)、是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ B A C = 90 ° ， A D$ 是 $B C$ 边上的高，E是 $B C$ 边上的一个动点（不与B，C重合）， $E F ⊥ A B ， E G ⊥ A C$ ，垂足分别为F，G．

(1)、求证： $\frac{E G}{A D} = \frac{C G}{C D}$ ；

(2)、 $F D$ 与 $D G$ 是否垂直？若垂直，请给出证明；若不垂直，请说明理由；

(3)、当 $A B = A C$ 时， $△ F D G$ 为等腰直角三角形吗？并说明理由．

查看试题解析