湘教版初中数学九年级下册1.4二次函数与一元二次方程的联系 同步练习
试卷更新日期:2021-12-20 类型:同步测试
一、单选题
-
1. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( )
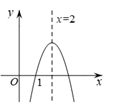
 A、 B、 C、 D、2. 如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=1,如果关于x的方程ax2+bx﹣6=0(a≠0)的一个根为2,那么该方程的另一个根为( )
A、 B、 C、 D、2. 如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=1,如果关于x的方程ax2+bx﹣6=0(a≠0)的一个根为2,那么该方程的另一个根为( ) A、﹣2 B、﹣1 C、0 D、33. 若函数y=ax2+bx的图象如图所示,则关于x的一元二次方程ax2+bx+5=0的根的情况为( )
A、﹣2 B、﹣1 C、0 D、33. 若函数y=ax2+bx的图象如图所示,则关于x的一元二次方程ax2+bx+5=0的根的情况为( ) A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根4. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(-1,0),给出下列结论:其中正确的个数是( )
A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根4. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(-1,0),给出下列结论:其中正确的个数是( )
①当x>0时,y随x的增大而减小;②am2+bm+c<a+b+c (m≠l);③b2-4ac<0;④当y>0时,-1<x<3;⑤2a+c>0
A、1个 B、2个 C、3个 D、4个5. 已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x , y)的对应值如表所示,则方程ax2+bx+2.32=0的根是( )x
……
0
4
……
y
……
0.32
﹣2
0.32
……
A、0或4 B、1或5 C、 或4﹣ D、 或 ﹣26. 如图所示二次函数y=ax2+bx+c的图象的一部分,图象过点(﹣3,0),对称轴为直线x=﹣1,以下结论:①2a﹣b=0;②abc<0;③当﹣3<x<1时,y>0;④对于a的每一个确定值,若一元二次方程ax2+bx+c=t(t为常数,t≥0)的根为整数,则t的值只有3个.其中正确的有( ) A、4个 B、3个 C、2个 D、1个7. 已知二次函数 ,其函数值y与自变量x之间的部分对应值如表所示:
A、4个 B、3个 C、2个 D、1个7. 已知二次函数 ,其函数值y与自变量x之间的部分对应值如表所示:x
…
0
1
2
3
…
y
…
1
2
1
-2
…
则方程 的正数解 在下列哪个范围内( )
A、 B、 C、 D、8. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣2,0),且对称轴为直线x=1,下列结论正确的是( )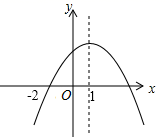 A、abc>0 B、关于x的一元二次方程ax2+bx+c=0的两根为3和﹣2 C、9a+c>3b D、当y>0时,x的取值范围是﹣2<x<49. 三个关于 的方程: ,已知常数 ,若 、 、 分别是按上顺序对应三个方程的正根,则下列判断正确的是( )A、 B、 C、 D、不能确定 的大小10. 若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )A、x1=﹣7,x2=3 B、x1=﹣6,x2=4 C、x1=6,x2=﹣4 D、x1=7,x2=﹣3
A、abc>0 B、关于x的一元二次方程ax2+bx+c=0的两根为3和﹣2 C、9a+c>3b D、当y>0时,x的取值范围是﹣2<x<49. 三个关于 的方程: ,已知常数 ,若 、 、 分别是按上顺序对应三个方程的正根,则下列判断正确的是( )A、 B、 C、 D、不能确定 的大小10. 若抛物线y=ax2+bx+c与x轴两个交点之间的距离为10,且4a+b=0,则关于x的方程ax2+bx+c=0的根为( )A、x1=﹣7,x2=3 B、x1=﹣6,x2=4 C、x1=6,x2=﹣4 D、x1=7,x2=﹣3二、填空题
-
11. 已知抛物线 的图像与x轴分别交于点 , ,则关于x的方程 的根为 .12. 二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),(t,4)三点,当t≥3时,一元二次方程ax2+bx+c=n一定有实数根,则n的取值范围是 .13. 已知点(1,0)是y=x2+bx﹣2的图象上一点,则方程x2+bx﹣2=0的根是 .14. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
 15. 已知二次函数 自变量x与函数值y之间满足下列数量关系:
15. 已知二次函数 自变量x与函数值y之间满足下列数量关系:…
…
…
…
则代数式 的值是 .
16. 若二次函数 的部分图象如图所示,则关于 的一元二次方程 的解为.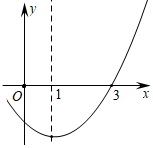
三、解答题
-
17. 抛物线y=﹣x2+bx+c(b , c为常数)与x轴交于点(x1 , 0)和(x2 , 0),与y轴交于点A , 点E为抛物线顶点.
(Ⅰ)当x1=﹣1,x2=3时,求点E , 点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.
18. 已知抛物线 经过 、 两点,求关于x的一元二次方程 的解.19. 二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,已知点A在点B的左侧,求点A和点B的坐标.20. 已知抛物线与x轴交于点 , ,与y轴交于点 ,该抛物线的顶点为D.(1)、求抛物线的解析式及其顶点D的坐标;(2)、直线 的解析式为;(3)、过点D作 轴于H , 在线段 上有一点P到直线 的距离等于线段 的长,求点P的坐标;(4)、设直线 交x轴于点E . 过点B作x轴的垂线,交直线 于点F , 将抛物线沿其对称轴平移,使平移后的抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?四、综合题
-
21. 在平面直角坐标系 中,已知抛物线 ( ).
 (1)、求抛物线的对称轴;(2)、若方程 ( )有两个不相等的实数根 , ,且 ,结合函数的图象,求 的取值范围.22. 如图, 二次函数 的图象与 轴分别交于点 (点 在点 的左侧), 且经过点 , 与 轴交于点 .
(1)、求抛物线的对称轴;(2)、若方程 ( )有两个不相等的实数根 , ,且 ,结合函数的图象,求 的取值范围.22. 如图, 二次函数 的图象与 轴分别交于点 (点 在点 的左侧), 且经过点 , 与 轴交于点 . (1)、求 的值.(2)、将线段 平移, 平移后对应点 和 都落在拋物线上, 求点 的坐标.
(1)、求 的值.(2)、将线段 平移, 平移后对应点 和 都落在拋物线上, 求点 的坐标.
