湘教版初中数学九年级下册1.1二次函数同步练习

试卷更新日期：2021-12-20 类型：同步测试

进入出卷网下载

一、单选题

1. 若函数 $y = (3 - 2 m) x^{m^{2} - 7} - x + 1$ 是二次函数，则m的值为（）

A、3 B、-3 C、 $\pm 3$ D、9

查看试题解析
2. 在下列关于x的函数中，一定是二次函数的是（）。

A、y=x² B、y=ax²+bx+c C、y=8x D、xy=1

查看试题解析
3. 若 $y = (m - 2) x^{2} - x + 1$ 是二次函数，则（）

A、 $m \neq 0$ B、 $m > 2$ C、 $m < 2$ D、 $m \neq 2$

查看试题解析
4. 某商品的进价为每件20元，现在的售价为每件40元，每星期可卖出200件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出5件．则每星期售出商品的利润y（单位：元）与每件涨价x（单位：元）之间的函数关系式是（）

A、y＝（200﹣5x）（40﹣20＋x） B、y＝（200＋5x）（40﹣20﹣x） C、y＝200（40﹣20﹣x） D、y＝200﹣5x

查看试题解析
5. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长），其余三边除大门外用栅栏围成，栅栏总长度为50m，门宽为2m．若饲养室长为xm，占地面积为ym² ，则y关于x的函数表达式为（）

A、y=- $\frac{1}{2}$ x²+26x（2≤x＜52） B、y=- $\frac{1}{2}$ x²+50x（2≤x＜52） C、y=-x²+52x（2≤x＜52） D、y=- $\frac{1}{2}$ x²+27x-52（2≤x＜52）

查看试题解析
6. 一个边长为2厘米的正方形，如果它的边长增加 $x (x > 0)$ 厘米，则面积随之增加 $y$ 平方厘米，那么 $y$ 与 $x$ 之间满足的函数关系是（）

A、正比例函数 B、反比例函数 C、一次函数 D、二次函数

查看试题解析
7. 下列函数中，是二次函数的有（）
① $y = 1 - \sqrt{2} x^{2}$ ② $y = \frac{1}{x^{2}}$ ③ $y = x (1 - x)$ ④ $y = (1 - 2 x) (1 + 2 x)$

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 在某种病毒的传播过程中，每轮传染平均1人会传染x个人，若最初2个人感染该病毒，经过两轮传染，共有y人感染.则y与x的函数关系式为（）

A、 $y = 2 {(1 + x)}^{2}$ B、 $y = {(2 + x)}^{2}$ C、 $y = 2 + 2 x^{2}$ D、 $y = {(1 + 2 x)}^{2}$

查看试题解析

二、填空题

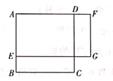
9. 关于x的函数 $y = (m + 2) x^{m^{2} - 2}$ 是二次函数，则m的值是.

查看试题解析
10. 如图，正方形ABCD的边长是4，E是AB上一点，F是AD延长线上的一点，BE=DF。若四边形AEGF是矩形，则矩形AEGF的面积y关于BE的长的函数解析式是(不用写出x的取值范围)

查看试题解析
11. 一个矩形的周长为16cm，设一边长为xcm，面积为y $c m^{2}$ ，那么y与x的关系式是

查看试题解析
12. 二次函数 $y = 2 x^{2} - 3 x - 1$ 的二次项系数与常数项的和是．

查看试题解析
13. 已知函数 $y = (m - 3) x^{2} - x + 5$ 是二次函数，则 $m$ 的取值范围是．

查看试题解析

三、解答题

14. 当m为何值时，函数 $y = (m + 1) x^{m^{2} - 2 m - 1} + 8 x - 1$ 是二次函数．

查看试题解析
15. 已知 $y = (m^{2} - m) x^{m^{2} - 2 m - 1} + (m - 3) x + m^{2}$ 是x的二次函数，求出它的解析式．

查看试题解析
16. 若函数y=（a-1）x^（^b+1^）+x²+1是二次函数，试讨论a、b的取值范围.

查看试题解析
17. 某商人如果将进货单价为8元的商品按每件10元出售，每天可售出100件，现在他采用提高售出价，减少进货量的办法增加利润，已知这种商品每提高1元，其销售量就要减少10件，如果他每天所赚利润为y元，试求出y与售出价x之间的函数关系式．

查看试题解析

四、综合题

18. 已知函数y=（m²-2）x²+（m+ $\sqrt{2}$ ）x+8．

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，求m的取值范围.

查看试题解析
19. 小李家用 $40 m$ 长的篱笆围成一个一边靠墙（墙足够长）的矩形菜园，如图.

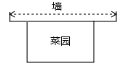(1)、写出这块菜园的面积 $y (m^{2})$ 与垂直于墙的边长 $x (m)$ 之间的函数解析式；

(2)、直接写出 $x$ 的取值范围.

查看试题解析
20. 若y=（m﹣3） $x^{m^{2} - 3 m + 2}$ 是二次函数，

(1)、求m的值．

(2)、求出该图象上纵坐标为﹣6的点的坐标．

查看试题解析
21. 某商场购进一种单价为40元的商品，如果以单价60元售出，那么每天可卖出300个，根据销售经验，每降价1元，每天可多卖出20个，假设每个降价x（元），每天销售y（个），每天获得利润W（元）．

(1)、写出y与x的函数关系式；

(2)、求出W与x的函数关系式（不必写出x的取值范围）

查看试题解析
22. 一条隧道的横截面如图所示，它的上部是一个半圆，下部是一个矩形，矩形的一边长为 $2.5$ 米．如果隧道下部的宽度大于 $5$ 米但不超过 $10$ 米，求隧道横截面积 $S$ （平方米）关于上部半圆半径 $r$ （米）的函数解析式及函数的定义域．

查看试题解析

湘教版初中数学九年级下册1.1二次函数 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

湘教版初中数学九年级下册1.1二次函数同步练习