初数浙教版九上二次函数y=ax2+bx+c的图象和性质及与y=a(x-h)2+k的转化 专项复习(普通版)
试卷更新日期:2021-12-20 类型:复习试卷
一、单选题
-
1. 抛物线 y=-2x2+8x-5 的对称轴是( )A、x=2 B、x=-2 C、x=4 D、x=-42. 关于二次函数y=x2﹣x的下列结论,错误的是( )A、图象的开口向上 B、当x<0时,y随x的增大而增大 C、图象经过点(2,2) D、图象的对称轴是直线x=3. 已知函数y=-x2+bx+c,其中b>0,c<0,此函数的图象可能是( )A、
 B、
B、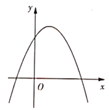 C、
C、 D、
D、 4. 二次函数y=x2﹣2x+4图象的顶点坐标是( )A、(1,3) B、(1,﹣3) C、(﹣1,3) D、(﹣1,﹣3)5. 若A(1, ),B(2, )是二次函数 图象上的两点,则 与 的大小关系是( )A、 < B、 = C、 > D、不能确定6. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( )
4. 二次函数y=x2﹣2x+4图象的顶点坐标是( )A、(1,3) B、(1,﹣3) C、(﹣1,3) D、(﹣1,﹣3)5. 若A(1, ),B(2, )是二次函数 图象上的两点,则 与 的大小关系是( )A、 < B、 = C、 > D、不能确定6. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( ) A、 B、 C、 D、7. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )
A、 B、 C、 D、7. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( ) A、3 B、4 C、5 D、68. 如图,二次函数 y=-x2+bx+c 图象上有三点 A(-1,y1 )、 B(1,y2) 、 C(2,y3) ,则 y1 ,y2 , y3大小关系为( )
A、3 B、4 C、5 D、68. 如图,二次函数 y=-x2+bx+c 图象上有三点 A(-1,y1 )、 B(1,y2) 、 C(2,y3) ,则 y1 ,y2 , y3大小关系为( ) A、 y1<y3<y2 B、y3 <y1<y2 C、 y1 <y2<y3 D、 y2<y1 <y39. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
A、 y1<y3<y2 B、y3 <y1<y2 C、 y1 <y2<y3 D、 y2<y1 <y39. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:x
……
-2
0
1
3
……
y
……
6
-4 -6
-4
……
下列各选项中,正确的是( )
A、这个函数的图象开口向下 B、这个函数的图象与x轴无交点 C、这个函数的最小值小于﹣6 D、当x>1时,y的值随x值的增大而增大10. 把y= x2﹣2x+1写成y=a(x﹣h)2+k的形式是( )A、 B、 C、 D、二、填空题
-
11. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0. 其中,正确的结论有 .
 12. 抛物线y=-3x2+6的顶点坐标为13. 二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:
12. 抛物线y=-3x2+6的顶点坐标为13. 二次函数y=ax2+bx+c(a≠0)的函数值y与自变量x之间的部分对应值如下表:x
…
﹣2
﹣1
0
1
2
…
y
…
﹣7
﹣1
3
5
5
…
则 的值为 .
14. 沿着x轴正方向看,抛物线y=x2-2在y轴左侧的部分是的(填“上升”或“下降”)15. 已知抛物线 的顶点在坐标轴上,则 .16. 如图,在平面直角坐标系中,抛物线y=x2﹣2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为 .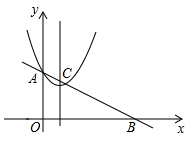
三、综合题
-
17. 已知二次函数 .(1)、求抛物线开口方向及对称轴.(2)、写出抛物线与y轴的交点坐标.18. 二次函数 的图象经过点(1,-8),(5,0).(1)、求b,c的值;(2)、求出该二次函数图象的顶点坐标和对称轴.19. 已知二次函数y=- x2+x+3 指出(1)、函数图象的对称轴和顶点坐标;(2)、把这个函数的图象向左、向下平移2个单位,得到哪一个函数的图象?(3)、该函数与Y轴的交点为A,与X轴的交点分别为B、C两点,求三角形ABC的面积?20. 如图,已知抛物线 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
 (1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.
(1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.