初数浙教版九上二次函数图象的几何变换专项复习（困难版）

试卷更新日期：2021-12-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 函数y＝﹣（x﹣2）²+1的图象可以由函数y＝﹣x²的图象通过（）得到

A、向左平移1个单位，再向上平移2个单位 B、向左平移1个单位，再向下平移2个单位 C、向右平移2个单位，再向上平移1个单位 D、向右平移2个单位，再向下平移1个单位

查看试题解析
2. 如图，反比例函数 $y_{1} = \frac{1}{x}$ 与二次函数 $y_{1} = {ax}^{2} + bx + c$ 图象相交于A、B、C三个点，则函数 $y = {ax}^{2} + bx - \frac{1}{x} + c$ 的图象与x轴交点的个数是 $($ $)$

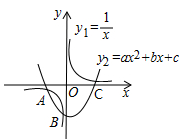A、0 B、1 C、2 D、3

查看试题解析
3. 将二次函数y＝﹣x²＋2x＋3的图象在x轴上方的部分沿x轴翻折后，所得新函数的图象如图所示.当直线y＝x＋b与新函数的图象恰有3个公共点时，b的值为（）

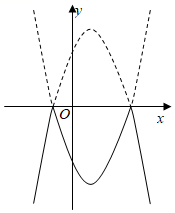A、 $- \frac{13}{4}$ 或﹣2 B、 $- \frac{21}{4}$ 或﹣2 C、 $- \frac{21}{4}$ 或﹣3 D、 $- \frac{13}{4}$ 或﹣3

查看试题解析
4. 如图，抛物线 $y = a x^{2} + 2 a x - 3 a$ （a＞0）与x轴交于A，B，顶点为点D，把抛物线在x轴下方部分关于点B作中心对称，顶点对应D′，点A对应点C，连接DD′，CD′，DC，当△CDD′是直角三角形时，a的值为（）

A、 $\frac{1}{2}$ 或 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{3}$ 或 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{3}$ 或 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$ 或 $\frac{\sqrt{3}}{3}$

查看试题解析
5. 把二次函数y＝ax²+bx+c（a＞0）的图象作关于x轴的对称变换，所得图象的解析式为y＝﹣a(x﹣1)²+2a，若(m﹣1)a+b+c≤0，则m的最大值是（）

A、0 B、1 C、2 D、4

查看试题解析

二、填空题

6. 把函数 $y = {(x - 1)}^{2} + 2$ 的图像向左平移1个单位长度，平移后的图像的函数解析式为．

查看试题解析
7. 把抛物线 $y = x^{2} - 4 x + 5$ 的图象先向右平移 $3$ 个单位长度，再向下平移 $2$ 个单位长度，所得新抛物线的解析式是．

查看试题解析
8. 将抛物线 $y = a x^{2} + b x - 1$ 向上平移3个单位长度后，经过点 $(- 2 ， 5)$ ，则8a-4b-11的值是．

查看试题解析
9. 如图，抛物线y＝﹣x²+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B.
①抛物线y＝﹣x²+2x+m+1与直线y＝m+2有且只有一个交点；

②若点M（﹣2，y₁）、点N（ $\frac{1}{2}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁＜y₂＜y₃；

③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）²+m；

④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\sqrt{34} + \sqrt{2}$ .

其中正确判断的序号是.

查看试题解析
10. 已知函数 $y = - \frac{1}{2} x^{2} + x + 4$ 与y轴交于点C ，顶点为D ．直线 $C D$ 交x轴于点E ，点F在直线 $C D$ 上，且橫坐标为4，现在，将抛物线沿其对称轴上下平移，使抛物线与线段 $E F$ 总有公共点．抛物线向上最多可以平移个单位长度，向下最多可以平移个单位长度．

查看试题解析

三、综合题

11. 如图，二次函数 $y = (x - 1) (x - a)$ （a为常数）的图象的对称轴为直线 $x = 2$ .

(1)、求a的值.

(2)、向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式.

查看试题解析
12. 甲秀楼是贵阳市一张靓丽的名片.如图①，甲秀楼的桥拱截面 $O B A$ 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽 $O A = 8 m$ ，桥拱顶点 $B$ 到水面的距离是 $4m$ .

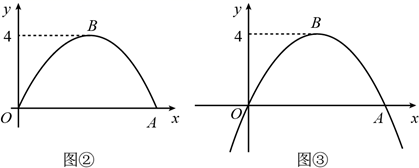(1)、按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；

(2)、一只宽为 $1 .2m$ 的打捞船径直向桥驶来，当船驶到桥拱下方且距 $O$ 点 $0 .4m$ 时，桥下水位刚好在 $O A$ 处.有一名身高 $1.68 m$ 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；

(3)、如图③，桥拱所在的函数图象是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，该抛物线在 $x$ 轴下方部分与桥拱 $O B A$ 在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移 $m (m > 0)$ 个单位长度，平移后的函数图象在 $8 \leq x \leq 9$ 时， $y$ 的值随 $x$ 值的增大而减小，结合函数图象，求 $m$ 的取值范围.

查看试题解析

初数浙教版九上二次函数图象的几何变换 专项复习（困难版）

一、单选题

二、填空题

三、综合题

初数浙教版九上二次函数图象的几何变换专项复习（困难版）