初数浙教版九上二次函数y=ax2、y=a(x-h)2+k的图象与性质专项复习（困难版）

试卷更新日期：2021-12-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列函数中，满足y的值随x的值增大而增大的是（　　）

A、y=﹣2x B、y=3x﹣1 C、y= $\frac{1}{x}$ D、y=x²

查看试题解析
2. 对于函数y=﹣2（x﹣m）²的图象，下列说法不正确的是（）

A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交

查看试题解析
3. 已知抛物线C：y＝ $\frac{1}{2}$ （x﹣1）²﹣1，顶点为D，将C沿水平方向向右（或向左）平移m个单位，得到抛物线C₁ ，顶点为D₁ ， C与C₁相交于点Q，若∠DQD₁＝60°，则m等于（）

A、±4 $\sqrt{3}$ B、±2 $\sqrt{3}$ C、﹣2或2 $\sqrt{3}$ D、﹣4或4 $\sqrt{3}$

查看试题解析
4. 已知点A(1，y₁),B(2,y₂)在抛物线y=-(x+1)²+2上，则下列结论正确的是（）

A、2>y₁>y₂ B、2>y₂>y₁ C、y₁>y₂>2 D、y₂>y₁>2

查看试题解析
5.
给出下列命题及函数 $y = x$ ， $y = x^{2}$ 和^{$y = \frac{1}{x}$}的图象
①如果 $\frac{1}{a} > a > a^{2}$ ，那么 $0 < a < 1$ ；
②如果 $a^{2} > a > \frac{1}{a}$ ，那么 $a > 1$ ；
③如果 $\frac{1}{a} > a^{2} > a$ ，那么 $- 1 < a < 0$ ；
④如果 $a^{2} > \frac{1}{a} > a$ 时，那么 $a < - 1$ .
则（）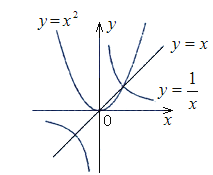

A、正确的命题是①④ B、错误的命题是②③④ C、正确的命题是①② D、错误的命题只有③

查看试题解析
6. 下列关系中，是二次函数关系的是（）

A、当距离S一定时，汽车行驶的时间t与速度v之间的关系。 B、在弹性限度时，弹簧的长度y与所挂物体的质量x之间的关系。 C、圆的面积S与圆的半径r之间的关系。 D、正方形的周长C与边长a之间的关系。

查看试题解析
7. 当-2≤x≤1时，二次函数y=-(x-m)²+m²+1有最大值4，则实数m的值为（）

A、 $- \frac{7}{4}$ B、 $\sqrt{3}$ 或- $\sqrt{3}$ C、2或- $\sqrt{3}$ D、2或 $\sqrt{3}$ 或 $- \frac{7}{4}$

查看试题解析
8. 如图，已知在平面直角坐标系xOy中，抛物线y= $\frac{13}{18} {(x-3)}^{2} - \frac{3}{2}$ 与y轴交于点A，顶点为B，直线l：y=- $\frac{4}{3}$ x+b经过点A，与抛物线的对称轴交于点C，点P是对称轴上的一个动点，若AP+ $\frac{3}{5}$ PC的值最小，则点P的坐标为（）

A、（3，1） B、（3， $\frac{11}{4}$ ） C、（3， $\frac{16}{5}$ ） D、（3， $\frac{12}{5}$ ）

查看试题解析
9. 已知函数 $y = {\begin{cases} {(x - 1)}^{2} - 1 (x \leq 3) \\ {(x - 5)}^{2} - 1 (x > 3) \end{cases}$ ，则使y=k成立的x值恰好有三个，则k的值为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 设抛物线y＝ax²(a＞0)与直线y＝kx＋b相交于两点，它们的横坐标为x₁ ， x₂ ，而x₃是直线与x轴交点的横坐标，那么x₁ ， x₂ ， x₃的关系是（）

A、x₃＝x₁＋x₂. B、x₃＝ $\frac{1}{x_{1}}$ ＋ $\frac{1}{x_{2}}$ . C、x₁x₂＝x₂x₃＋x₃x₁. D、x₁x₃＝x₂x₃＋x₁x₂.

查看试题解析

二、填空题

11. 已知二次函数 $y = a {(x + 2)}^{2} + b$ 有最大值 $\frac{1}{2}$ ，则 $a$ ， $b$ 的大小关系为．

查看试题解析
12. 如图，抛物线y₁=a（x+2）²+m过原点，与抛物线y₂= $\frac{1}{2}$ （x﹣3）²+n交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．下列结论：①两条抛物线的对称轴距离为5；②x=0时，y₂=5；③当x＞3时，y₁﹣y₂＞0；④y轴是线段BC的中垂线．正确结论是（填写正确结论的序号）．

查看试题解析
13. $y = - 2 {(x - 1)}^{2} + 5$ 的图象开口向，顶点坐标为，当 $x > 1$ 时， $y$ 值随着 $x$ 值的增大而．

查看试题解析
14. 农机厂第一个月水泵的产量为50（台），第三个月的产量y（台）与月平均增长率x之间的关系表示为．

查看试题解析
15. 已知函数 $y = {\begin{matrix} {(x - 1)}^{2} - 1 & (x \leq 3) \\ {(x - 5)}^{2} - 1 & (x > 3) \end{matrix}$ ，若使y＝k成立的x值恰好有三个，则k的值为．

查看试题解析
16. 已知二次函数y=a（x﹣1）²﹣2（a≠0）的图象在﹣1＜x＜0这一段位于x轴下方，在3＜x＜4这一段位于x轴的上方，则a的值为．

查看试题解析
17. 如图，已知正方形OBCD的三个顶点坐标分别为B(1，0)，C(1，1)， D(0，1). 若抛物线 $y = {(x - h)}^{2}$ 与正方形OBCD的边共有3个公共点，则h的取值范围是.

查看试题解析
18.
如图，有四张不透明的卡片除正面的函数关系式不同外，其余相同，将它们背面朝上洗匀后，从中抽取一张卡片，则抽到函数图象不经过第四象限的卡片的概率为．

查看试题解析

三、综合题

19. 已知函数y=-(m+2) $x^{m^{2} - 2}$ (m为常数)，求当m为何值时：

(1)、y是x的一次函数?

(2)、y是x的二次函数?并求出此时纵坐标为-8的点的坐标.

查看试题解析
20.
如图，抛物线y=﹣（x﹣1）²+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．

(1)、求点B，C的坐标；

(2)、判断△CDB的形状并说明理由；

(3)、将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．

查看试题解析
21.
如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A、B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y= $\frac{3}{4}$ x+4，与x轴相交于点D，以点C为顶点的抛物线过点B．

(1)、求抛物线的解析式；

(2)、判断直线l与⊙E的位置关系，并说明理由；

(3)、动点P在抛物线上，当点P到直线l的距离最小时．求出点P的坐标及最小距离．

查看试题解析
22. 已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B(点A在点B左侧)，根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”。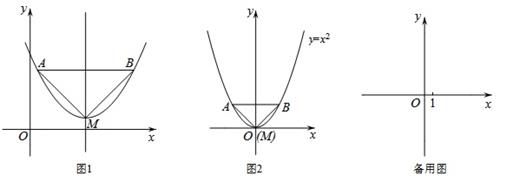

(1)、①如图2，求出抛物线y=x²的“完美三角形”斜边AB的长；
②请写出一个抛物线的解析式，使它的完美三角形与y=x²+1的“完美三角形”全等；

(2)、若抛物线y=ax²+4的“完美三角形”的斜边长为4，求a的值；

(3)、若抛物线y=mx²+2x+n−5的“完美三角形”斜边长为n，且y=mx²+2x+n−5的最大值为−1，求m，n的值。

查看试题解析
23. 如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC

(1)、求线段OC的长度；

(2)、设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；

(3)、在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析

初数浙教版九上二次函数y=ax2、y=a(x-h)2+k的图象与性质 专项复习（困难版）

一、单选题

二、填空题

三、综合题

初数浙教版九上二次函数y=ax2、y=a(x-h)2+k的图象与性质专项复习（困难版）