初数浙教版九上二次函数y=ax2、y=a(x-h)2+k的图象和性质 专项复习(普通版)
试卷更新日期:2021-12-20 类型:复习试卷
一、单选题
-
1. 下列函数中,正比例函数是( )A、y=﹣8x B、y= C、y=8x2 D、y=8x﹣42. 二次函数y=(x-1)2+3图象的顶点坐标是( )A、(1,3) B、(1,-3) C、(-1,3) D、(-1,-3)3. 二次函数 的一次项系数是( )A、1 B、-1 C、2 D、-24. 若二次函数 的图像经过原点,则m的值为( )
A、2 B、0 C、2或0 D、15. 对于二次函数y=−(x−1)2+2的图象与性质,下列说法正确的是( )
A、对称轴是直线x=1,最小值是2 B、对称轴是直线x=1,最大值是2 C、对称轴是直线x=−1,最小值是2 D、对称轴是直线x=−1,最大值是26. 下列函数关系中,不属于二次函数的是( )
A、 B、 C、 D、7. 二次函数 与一次函数 在同一坐标系中的大致图象可能是( )A、 B、
B、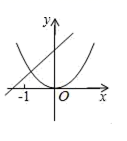 C、
C、 D、
D、 8. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、9. 已知点 , 是抛物线 图像上的两点,则以下结论正确的是( )A、 B、 C、 D、10. 对于二次函数y=﹣3(x+2k)2+k(a≠0)而言,无论k取何实数,其图象的顶点都在( )A、x轴上 B、直线y=﹣x上 C、直线y= x D、直线y= x上
8. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、9. 已知点 , 是抛物线 图像上的两点,则以下结论正确的是( )A、 B、 C、 D、10. 对于二次函数y=﹣3(x+2k)2+k(a≠0)而言,无论k取何实数,其图象的顶点都在( )A、x轴上 B、直线y=﹣x上 C、直线y= x D、直线y= x上二、填空题
-
11. 二次函数y=x2的图象是一条 , 它的开口向 , 它的对称轴为 , 它的顶点坐标为 .
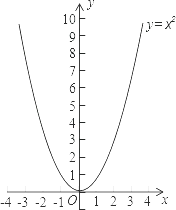 12. 已知二次函数y= (x-m)2+m2+1,且 .(1)、当m=1时,函数y有最大值.(2)、当函数值y恒不大于4时,实数m的范围为.13. 如图,二次函数y=(x﹣1)2﹣1的图象(0≤x≤3),y的取值范围是.
12. 已知二次函数y= (x-m)2+m2+1,且 .(1)、当m=1时,函数y有最大值.(2)、当函数值y恒不大于4时,实数m的范围为.13. 如图,二次函数y=(x﹣1)2﹣1的图象(0≤x≤3),y的取值范围是. 14. 若抛物线y=2(x-2)2+k过原点,则该抛物线与x轴的另一个交点坐标为15. 已知一个函数,当 时,函数值 随着 的增大而减小,请写出这个函数关系式(写出一个即可).16. 抛物线 有最点,其坐标是 , 当x时,y随x的增大而减小.17. 如图,四个函数的图象中,分别对应的是:①y=ax2;②y=bx2;③y=cx2;④y=dx2 . 则a、b、c、d的大小关系为 .
14. 若抛物线y=2(x-2)2+k过原点,则该抛物线与x轴的另一个交点坐标为15. 已知一个函数,当 时,函数值 随着 的增大而减小,请写出这个函数关系式(写出一个即可).16. 抛物线 有最点,其坐标是 , 当x时,y随x的增大而减小.17. 如图,四个函数的图象中,分别对应的是:①y=ax2;②y=bx2;③y=cx2;④y=dx2 . 则a、b、c、d的大小关系为 .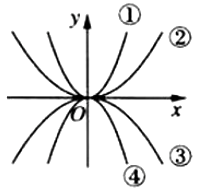
18. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形的边有公共点,则实数a的取值范围是 .
三、综合题
-
19. 已知函数 是二次函数.(1)、求m的值;(2)、求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.20. 已知 是二次函数,且函数图象有最高点.
(1)、求k的值;(2)、求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.21. 某农作物的生长率 与温度 ( )有如下关系:如图1,当10≤ ≤25 时可近似用函数 刻画;当25≤ ≤37 时可近似用函数 刻画.
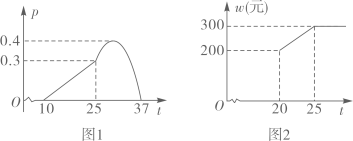 (1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系:
(1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系:生长率
0.2
0.25
0.3
0.35
提前上市的天数 (天)
0
5
10
15
①请运用已学的知识,求 关于 的函数表达式;
②请用含 的代数式表示
(3)、天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本 (元)与大棚温度 ( )之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).22. 若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.(1)、请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;(2)、已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.23. 如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题: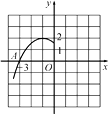 (1)、抛物线与x轴的一个交点A的坐标是 , 则抛物线与x轴的另一个交点B的坐标是;(2)、确定a的值;(3)、设抛物线的顶点是P,试求△PAB的面积.
(1)、抛物线与x轴的一个交点A的坐标是 , 则抛物线与x轴的另一个交点B的坐标是;(2)、确定a的值;(3)、设抛物线的顶点是P,试求△PAB的面积.