湘教版初中数学七年级上学期期末复习专题13 线段射线直线
试卷更新日期:2021-12-18 类型:复习试卷
一、单选题
-
1. 已知点C是线段AB的中点,下列说法:①AB=2AC;②BC= AB;③AC=BC.其中正确的个数是( )A、0 B、1 C、2 D、32. 如图,数轴上A、B两点之间的距离是3,点B在点A左侧,那么点B表示的数是( )
 A、3 B、﹣3 C、1 D、﹣13. 将 , , , 这四个数分别用点表示在数轴上,其中与 所表示的点最近的数是( )A、 B、 C、 D、4. 如图,从小明家A到学校B原有三条路线:路线①A﹣D﹣B;路线②A﹣E﹣B;路线③A﹣C﹣B , 后又开通了一条直道,路线④A﹣B , 这四条路线中路程最短的是( )
A、3 B、﹣3 C、1 D、﹣13. 将 , , , 这四个数分别用点表示在数轴上,其中与 所表示的点最近的数是( )A、 B、 C、 D、4. 如图,从小明家A到学校B原有三条路线:路线①A﹣D﹣B;路线②A﹣E﹣B;路线③A﹣C﹣B , 后又开通了一条直道,路线④A﹣B , 这四条路线中路程最短的是( )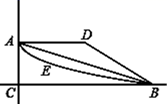 A、路线① B、路线② C、路线③ D、路线④5. 在数轴上与点-3的距离等于4的点表示的数是( )A、1 B、1或-7 C、-7 D、-1或76. 点 在数轴上表示的数为-3,若一个点从点 移动4个单位长度,此时终点所表示的数是( )A、-7或-1 B、1 C、7 D、1或-77. 如图,C,B是线段AD上的两点,若 , ,则AC与CD的关系为( )
A、路线① B、路线② C、路线③ D、路线④5. 在数轴上与点-3的距离等于4的点表示的数是( )A、1 B、1或-7 C、-7 D、-1或76. 点 在数轴上表示的数为-3,若一个点从点 移动4个单位长度,此时终点所表示的数是( )A、-7或-1 B、1 C、7 D、1或-77. 如图,C,B是线段AD上的两点,若 , ,则AC与CD的关系为( ) A、 B、 C、 D、不能确定8. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( )
A、 B、 C、 D、不能确定8. 如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是( ) A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短9. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )
A、两点之间,直线最短 B、经过一点,有无数条直线 C、两点确定一条直线 D、两点之间,线段最短9. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )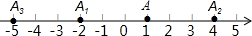 A、9 B、10 C、11 D、1210. 线段 ,点 是线段 上的一个动点(与点 、 不重合),点 是线段 的中点,点 是线段 的中点,则线段 的长是( )A、 B、 C、 D、无法确定
A、9 B、10 C、11 D、1210. 线段 ,点 是线段 上的一个动点(与点 、 不重合),点 是线段 的中点,点 是线段 的中点,则线段 的长是( )A、 B、 C、 D、无法确定二、填空题
-
11. 已知点C是直线AB上一点,且AC:BC=7:3,若AB=10,则AC= .12. 如图,C,D是线段AB上两点,CB=3cm,DB=5cm,D是AC的中点,则线段AB的长为cm.
 13. 在数轴上表示点 的数是 ,则与点 相距 个单位长度的点表示的数是 .14. 数轴上点P与原点距离为3,点Q与点P的距离为3,则点Q所表示的数为15. 在数轴上,当单位长度是1时,到表示-2的点的距离等于5个单位长度的点表示的数是 .16. 数轴上与原点的距离是6个单位长度的点表示的数是 .
13. 在数轴上表示点 的数是 ,则与点 相距 个单位长度的点表示的数是 .14. 数轴上点P与原点距离为3,点Q与点P的距离为3,则点Q所表示的数为15. 在数轴上,当单位长度是1时,到表示-2的点的距离等于5个单位长度的点表示的数是 .16. 数轴上与原点的距离是6个单位长度的点表示的数是 .三、作图题
-
17. 尺规作图:
已知:如图,线段AB.
求作:线段 ,使 .
 18. 如图,已知四点A,B,C,D,请用直尺按要求完成作图.
18. 如图,已知四点A,B,C,D,请用直尺按要求完成作图.( 1 )作射线AD;
( 2 )作直线BC;
( 3 )连接BD,请在BD上确定点P,使AP+CP的值最小,并说明理由.

四、解答题
-
19. 如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.若AC=9,BC=6,求线段MN的长.
 20. 如图所示,有理数a,b,c在数轴上的对应点分别是A、B、C,原点为点O.
20. 如图所示,有理数a,b,c在数轴上的对应点分别是A、B、C,原点为点O.①化简:|a﹣c|+2|c﹣b|﹣|b﹣a|.
②若B为线段AC的中点,OA=6,OA=4OB,求c的值.
 21. 如图所示,在△ABC中,∠ACB=90°,AB=25,AC=24,AM=AC,BN=BC,求MN的长。
21. 如图所示,在△ABC中,∠ACB=90°,AB=25,AC=24,AM=AC,BN=BC,求MN的长。
五、综合题
-
22. 如图,点A在数轴上所对应的数为2,
 (1)、点B在点A左侧且距点A为3个单位长度,则点B所对应的数为 , 请在数轴上标出点B的位置;(2)、在(1)的条件下,点A以每秒1个单位长度沿数轴向右运动,点B以每秒2个单位长度沿数轴向左运动,当点A运动到5所在的点处时停止运动,同时点B也停止运动,求此时A,B两点间距离;(3)、在(2)的条件下,若点A不动,点B沿数轴向右运动,经过t秒A,B两点相距3个单位长度,求t值;(4)、在(1)的条件下,点A以每秒1个单位长度,点B以每秒2个单位长度同时沿数轴向左运动,当点B运动到所对应的数为m时停止运动,请直接写出此时点A所对应的数为;若点A继续运动,请直接写出当AB=2时,点A继续运动的距离为 .(用含m的式子表示)
(1)、点B在点A左侧且距点A为3个单位长度,则点B所对应的数为 , 请在数轴上标出点B的位置;(2)、在(1)的条件下,点A以每秒1个单位长度沿数轴向右运动,点B以每秒2个单位长度沿数轴向左运动,当点A运动到5所在的点处时停止运动,同时点B也停止运动,求此时A,B两点间距离;(3)、在(2)的条件下,若点A不动,点B沿数轴向右运动,经过t秒A,B两点相距3个单位长度,求t值;(4)、在(1)的条件下,点A以每秒1个单位长度,点B以每秒2个单位长度同时沿数轴向左运动,当点B运动到所对应的数为m时停止运动,请直接写出此时点A所对应的数为;若点A继续运动,请直接写出当AB=2时,点A继续运动的距离为 .(用含m的式子表示)
