湘教版初中数学七年级上学期期末复习专题11 一元一次方程模型的应用
试卷更新日期：2021-12-18 类型：复习试卷
一、单选题
-
1. 如图，表中给出的是某月的月历，任意选取“H"型框中的7个数（如阴影部分所示），请你运用所学的数学知识来研究，发现这7个数的和不可能的是（ ）
A、63 B、70 C、96 D、1052. 幻方，又称纵横图．如图1是由数字1~9九个整数按照一定的规律排列成三行三列的一个方阵，每一横行、每一竖列以及两条斜线上的点数的和都相等．如图2所示的幻方中给出了三个数，则P处应该填的数字是（ ）
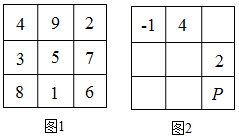A、－1 B、0 C、1 D、23. 如图，表中给出的是某月的月历，任意选取“U”型框中的5个数（如阴影部分所示），请你运用所学的数学知识来研究，在本月历中这5个数的和可能的是（ ）
A、64 B、75 C、91 D、1244. 做完了一天的功课，立新老师组织学生乘坐小船泛游包河公园，若租用10座的小船m艘，则余下8人无座位：若租用16座的小船则可少租用1艘，且最后一艘小船还没坐满，则乘坐最后一艘16座小船的人数是（ ）A、32-6m B、40-6m C、64-8m D、16-2m5. 一轮船航行于两个码头之间，逆水航行需10小时，顺水航行需6小时，已知水流的速度为每小时航行8千米，则两码头间的距离为（ ）千米A、480 B、540 C、240 D、2806. 如图，边长为 的正方形纸片，剪出一个边长为a的正方形之后，剩余部分可剪拼成一个长方形（不重叠无缝隙），若拼成长方形的一边长为3，则另一边长是（ ）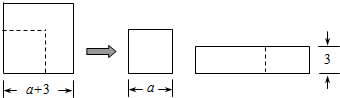
A、 B、 C、 D、7. 一架飞机在两城间飞行，顺风航行要5.5小时，逆风航行要6小时，风速为24千米/时，设飞机无风时的速度为每小时x千米，则下列方程正确的是（ ）A、 B、 C、 D、8. 某商店在某一时间以每件100元的价格卖出两件衣服，其中一件盈利25%，另一件亏损20%，则该商店卖出这两件衣服的盈亏情况为（ ）A、不盈也不亏 B、盈利5元 C、亏损5元 D、盈利10元9. 向含盐80%的5千克盐水中加水，制成含盐20%的盐水，需加水多少千克？（ ）A、15 B、20 C、2510. 如图，已知纸面上有一数轴，折叠纸面，使-3表示的点与1表示的点重合，则与-5表示的点重合的点表示的数是（ ）
A、3 B、4 C、5 D、-1二、填空题
-
11. 用大小两台拖拉机耕地．每小时共耕地30亩，已知大拖拉机的效宰是小拖拉机的1.5倍，问小拖拉机每小时耕地多少亩？设小拖拉机每小时耕地x亩．根据题意可列方程：12. 停车场上停着三轮车和小汽车共12辆，一共有41个车轮，三轮车有辆．13. 下面是王刚和李明两位同学的行程图，如果两人同时在同一地点出发，沿着200米的环形跑道同向行走，那么分钟后两人首次相遇．
14. 幻方历史悠久，传说最早出现在夏禹时代的“洛书”当中．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1～9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则m的值为 ．
15. 《九章算术》第八卷《方程》记载：“今有六雀七燕，集称之衡，雀俱重，燕俱轻，一雀一燕交而处，衡视平.”意为：六只雀比七只燕重，若将这群雀和这群燕互相交换一只以后，两群鸟一样重，假设一只燕重a克，则用含a的式子表示一只雀的重量为克．16. 一项工程甲队单独完成此项工程需60天，甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 ．若由甲队先做10天，剩下的工程再由甲、乙两队合作 天可以完成此项工程．三、解答题
-
17. 2021年！1月1日，某社区接种新冠疫苗第二针(分为北京科兴和北京生物两种)人数共110人，其中接种北京科兴的人数是接种北京生物的人数的2倍多20人，求接种两种疫苗的人数分别是多少人？18. 一辆快车和一辆慢车同时从甲、乙两地相对开出，3小时后在距离中点48千米处相遇，已知慢车速度是快车的 ，求甲、乙两地相距多少千米？19. 实验学校组织秋游，如果用45座的客车若干辆，则15人没有座位；如果用同样数量的60座客车，则多出一辆，且其余全部坐满．参加秋游的学生一共有多少名？
四、综合题
-
20. 如图为2021年11月的日历：
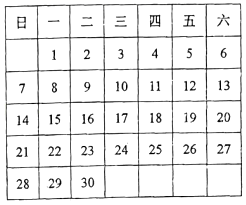(1)、在日历上任意圈出一个竖列上相邻的3个数：①设中间的一个数为a，则另外的两个数为 ， ；
②若已知这三个数的和为60，则这三个数在星期 ．
(2)、在日历上用一个小正方形任意圈出其中的9个数，设圈出的9个数的中心的数为b，若这9个数的和为153，求b2﹣1的值．21. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．结合数轴与绝对值的知识回答下列问题：
(1)、探究：①数轴上表示1和6的两点之间的距离是；
②数轴上表示﹣2和7的两点之间的距离是；
③数轴上表示﹣9和﹣3的两点之间的距离是 ．
(2)、归纳：数a和数b的两点之间的距离可以表示为 ．
(3)、应用：如果数a和3的两点之间的距离是15，则可记为：|a﹣3|＝15，那么a的值为多少．
22. 阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；
②如图3，点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；
③如图4，点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|
回答下列问题：
(1)、数轴上表示2和5的两点之间的距离是 ， 数轴上表示﹣2和﹣5的两点之间的距离是 ， 数轴上表示1和﹣3的两点之间的距离是；(2)、数轴上表示x和﹣1的两点A和B之间的距离是 ， 如果|AB|＝2，那么x为；(3)、代数式|x+1|+|x﹣2|取最小值时，相应的整数x的取值是 ．