湘教版初中数学七年级上学期期末复习专题10 等式的性质与一元一次方程的解法

试卷更新日期：2021-12-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各式进行的变形中，错误的是（）

A、若 $3 a = 2 b$ ，则 $3 a + 2 = 2 b + 2$ B、若 $3 a = 2 b$ ，则 $3 a - 5 = 2 b - 5$ C、若 $3 a = 2 b$ ，则 $\frac{a}{2} = \frac{b}{3}$ D、若 $3 a = 2 b$ ，则 $9 a = 4 b$

查看试题解析
2. 一元一次方程x+3x=8的解是（）

A、x=-1 B、x=0 C、x=1 D、x=2

查看试题解析
3. 已知整式2y²-3y+4的值是12，那么整式y²- $\frac{3}{2}$ y-1的值是（）

A、3 B、-3 C、5 D、7

查看试题解析
4. 下列式子的变形中，正确的是（）

A、 $6 + x = 7$ 得 $x = 7 + 6$ B、 $3 x + 2 = 5 x$ 得 $3 x - 5 x = 2$ C、 $2 x = 3$ 得 $x = \frac{2}{3}$ D、 $2 x + 4 = 2$ 得 $x + 2 = 1$

查看试题解析
5. 下列等式的变形中，正确的是（）

A、如果 $\frac{a}{c} = \frac{b}{c}$ ，那么a=b B、如果|a|=|b|，那么a=b C、如果ax =ay ，那么x= y D、如果a=b ，那么 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
6. 在解关于x的方程 $\frac{2 x -1}{3} = \frac{x + a}{2} - 2$ 时，小冉在去分母的过程中，右边的“-2”漏乘了公分母6，因而求得方程的解为x=2，则方程正确的解是（）

A、x=-12 B、x=-8 C、x=8 D、x=12

查看试题解析
7. 已知等式3a＝2b+5，则下列等式变形错误的是（　　）

A、3a﹣5＝2b B、3a+1＝2b+6 C、a＝ $\frac{2}{3}$ b+ $\frac{5}{3}$ D、3ac＝2bc+5

查看试题解析
8. 下列等式变形中，正确的是（）

A、若a=b，则a-3=3-b B、若 $\frac{x}{a} = \frac{y}{a}$ ，则x=y C、若ac=bc，则a=b D、若 $\frac{b}{a} = \frac{d}{c}$ ，则b=d

查看试题解析
9. 若a＝b ，下列等式不一定成立的是（　　）

A、a+5＝b+5 B、a﹣5＝b﹣5 C、ac＝bc D、 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
10. 在解方程 $\frac{x - 1}{2} - \frac{2 x + 3}{3} = 1$ 时，去分母正确的是（）

A、 $3 (x - 1) - 2 (2 x + 3) = 1$ B、 $3 (x - 1) + 2 (2 x + 3) = 1$ C、 $3 (x - 1) - 2 (2 + 3 x) = 6$ D、 $3 (x - 1) - 2 (2 x + 3) = 6$

查看试题解析

二、填空题

11. 如图，点C，D在线段AB上，且AD＝BC，则ACBD（填“＞”、“＜”或“＝”）．

查看试题解析
12. 若|x+2022|＝2，则x的值为．

查看试题解析
13. 若a=b+5，则a-b=

查看试题解析
14. 在△ABC中，若∠A：∠B：∠C=2：3：4，则∠C的度数是

查看试题解析
15. 绝对值拓展材料：|a|表示数a在数轴上的对应点与原点的距离如：|5|表示5在数轴上的对应点到原点的距离而|5|＝|5﹣0|，即|5﹣0表示5、0在数轴上对应的两点之间的距离类似的，有：|5+3|＝|5﹣（﹣3）|表示5、﹣3在数轴上对应的两点之间的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a﹣b|．
完成下列题目：

(1)、A、B分别为数轴上两点，A点对应的数为﹣2，B点对应的数为4
①A、B两点之间的距离为；

②折叠数轴，使A点与B点重合，则表示﹣3的点与表示的点重合；

③若在数轴上存在一点P到A的距离是点P到B的距离的2倍，则点P所表示的数是；

(2)、若满足|x﹣2|+|x+3|＝6时，则x的值是．

查看试题解析
16. 小明做了这样一道计算题： $| (- 3) + ■ |$ ，其中“ $■$ ”表示被墨水污染看不到的个数，他分析了后边的答案得知该题的计算结果为5，那么“ $■$ ”表示的应该是.

查看试题解析

三、计算题

17. 解方程：

(1)、 $3 x - 5 = 8$

(2)、 $- 2 x + 3 = 4 x - 9$

(3)、 $3 (x + 2) - 2 (x + 2) = 2 x + 4$

(4)、 $\frac{3 y - 1}{4} - 1 = \frac{5 y - 7}{6}$

查看试题解析

四、解答题

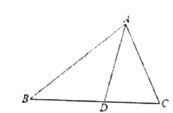
18. 当y取何值时，式子3y+4的值比2y-7的值大3？

查看试题解析
19. 如图，△ABC中，AD是∠BAC的平分线，∠B=∠DAC，∠C=2∠B，求∠ADB的度数．

查看试题解析
20. 有一架秋千，当它静止时，踏板离地的垂直高度DE=0.5m，将它往前推送2m(水平距离BC=2m)时，秋千的踏板离地的垂直高度BF=1.5m，秋千的绳索始终拉得很直，求绳索AD的长度

查看试题解析

五、综合题

21. 如图，点A、B、C是数轴上三点，点A、B、C表示的数分别为-10、2、6，我们规定：数铀上两点之间的距离用字母表示．例如：点A与点B之间的距离，可记为AB

(1)、写出AB= ， BC= ，AC=

(2)、点P是A、C之间的点，点P在数轴上对应的数为x
①若PB=5时，则x=

②PA = ， PC= (用含x的式子表示)；

(3)、动点M、N同时从点A、C出发，点M以每秒2个单位长度的速度沿数轴向右运动，点N以每秒2个单位长度的速度沿数向左运动，设运动时间为t(t>0)秒，求当t为何值时，点M、N之间相距2个单位长度？

查看试题解析
22. 规定一种新的运算：a※b=a- 2b，例如：3※2=3-2×2=-1．根据新运算法则，解答下列问题：

(1)、求(-2)※5的值；

(2)、若2※(x+1)=10，求x的值．

查看试题解析
23. 在学习整式加减法时，小明同学做了这样一道题目：
化简：(2x²+ax)-(-2x²+ax+1)

=2x²+ax+2x²-ax-1

=(2+2)x²+(a-a)x-1

=4x²-1

小明发现，化简后含x项的系数和为0，所以整式(2x²+ax)-(-2x²+ax+1)的值和a的取值无关．请根据小明发现的规律，解决下列问题．

已知整式2(ax³+2bx²+1)-4(-x³-3x²+6)的值与a、b的取值无关，回答下列问题：

(1)、直接写出a= ， b=

(2)、求整式2ab²+3a³b的值

(3)、解关于x的方程： $\frac{x + a}{2} - \frac{x + b}{3} = 1$

查看试题解析