湘教版初中数学七年级上学期期末复习专题5 有理数的乘方及其混合运算

试卷更新日期：2021-12-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 用四舍五入法取近似数：7.8963（精确到0.01）≈（）

A、 $7 .90$ B、 $7 .80$ C、 $7.89$ D、 $8.00$

查看试题解析
2. 下列各组数中，数值相等的是（）

A、 $- 3 \times 2^{3}$ 与 $- 3^{2} \times 2$ B、 $- 3^{2}$ 与 ${(- 3)}^{2}$ C、 $- 2^{5}$ 与 ${(- 2)}^{5}$ D、 ${(- \frac{2}{3})}^{2}$ 与 ${(- \frac{3}{2})}^{3}$

查看试题解析
3. 2021年1月4日，2021年全国邮政管理工作会议在北京召开．会议指出，2020年全年快递业务量和业务收入分别完成830亿件和8750亿元，同比分别增长30.8%和16.7%．其中8750亿用科学记数法可表示为（）

A、8.3×10¹⁰ B、830×10⁸ C、875×10⁹ D、8.75 ×10¹¹

查看试题解析

4. 北京市居民用水实行阶梯水价，实施细则如下表：

分档水量	年用水量（立方米）	水价（元/立方米）
第一阶梯	0－180（含180）	5.00
第二阶梯	180－260（含260）	7.00
第三阶梯	260以上	9.00

若某户2020年共用水280立方米，则应交水费为（）

A、1150元 B、1250元 C、1640元 D、2070元

查看试题解析

5. 我国森林覆盖面积约为1340000平方千米，这个数字用科学记数法表示为（）

A、 $1.34 \times 10^{6}$ B、 $13.4 \times 10^{5}$ C、 $1.34 \times 10^{8}$ D、 $1.34 \times 10^{9}$

查看试题解析
6. 下列式子中，正确的是（）

A、 ${(- 2)}^{3} = {(- 3)}^{2}$ B、 ${(- 6)}^{2} = 12$ C、 $- 5^{3} = {(- 5)}^{3}$ D、 $- \frac{3^{2}}{5} = - \frac{6}{5}$

查看试题解析
7. 计算 $- \frac{2^{2}}{3}$ 的结果是 $($ $)$

A、 $- \frac{4}{3}$ B、 $- \frac{4}{9}$ C、 $\frac{4}{3}$ D、 $\frac{4}{9}$

查看试题解析

8. 某路公交车从起点经过

A

，

B

，

C

，

D

站到达终点，各站上、下乘客人数如下表所示（用正数表示上车的人数，负数表示下车的人数）

站点	起点	$A$	$B$	$C$	$D$	终点
上车人数	$x$	15	12	7	5	0
下车人数	0	$- 3$	$- 4$	$- 10$	$- 11$	$- 29$

若此公交车采用一票制，即每位上车乘客无论哪站下车，车票都是2元，问该车这次出车共收入（）

A、114元 B、228元 C、78元 D、56元

查看试题解析

9. 人民网北京2021年1月7日电，截至1月3日6时，我国首次火星探测任务“天问一号”火星探测器已经在轨飞行约163天，飞行里程突破4亿公里，距离地球接近1.3亿公里，距离火星约830万公里．若对后两个数据中的一个用科学记数法表示，则正确的是（）

A、1.3×10⁹公里 B、13×10⁸公里 C、8.3×10⁶公里 D、8.3×10⁵公里

查看试题解析
10. 13世纪数学家斐波那契的《计划书》中有这样一个问题：“在罗马有7位老妇人，每人赶着7头毛驴，每头驴驮着7只口袋，每只口袋里装着7个面包，每个面包附有7把餐刀，每把餐刀有7只刀鞘”，则刀鞘数为（）

A、42 B、49 C、 $7^{6}$ D、 $6^{7}$

查看试题解析

二、填空题

11. 2021年5月19日，第三届阿里数学竞赛预选赛顺利结束，本届大赛在全球范围内吸引了约5万名数学爱好者参加，阿里数学竞赛旨在全球范围内引领开启关注数学、理解数学、欣赏数学、助力数学的科学风尚.5万用科学记数法表示为．

查看试题解析
12. 下列数： $- (+ 5) ， {(-2)}^{3} ， - {(-1)}^{100} ， 0 ， {(- \frac{1}{7})}^{2} ， | -0 .6 |$ ，其中负数有个。

查看试题解析
13. 对于近似数 $0.1998$ ，精确到 $0.01$ 表示为．

查看试题解析
14. 一个有理数的平方等于 $100$ ，则这个有理数是．

查看试题解析
15. 截止2021年10月20日，电影《长津湖》的累计票房达到大约50.36亿元，数据50.36亿用科学记数法表示为．

查看试题解析
16. 《福建省新冠病毒疫苗接种工作方案》指出：经测算，人群接种率需达到77.6%以上，才能建立免疫屏障，福建省需完成约6000万剂次（每人接种2剂次）的疫苗接种．数据60000000用科学记数法表示为．

查看试题解析

三、计算题

17.

(1)、计算： $- (3 - 5) + {(- 3)}^{2} \times (1 - 3)$

(2)、计算： $- 2^{4} + (\frac{1}{4} - \frac{5}{9} + \frac{7}{12}) \times (- 72)$

查看试题解析
18. 计算：

(1)、 ${(- 1)}^{2021} - \frac{1}{4} \times [2 - {(- 3)}^{2}]$

(2)、 $(\frac{1}{4} + \frac{1}{6} - \frac{1}{2}) \times 12 + {(- 2)}^{3} \div (- 4)$ ．

查看试题解析

四、解答题

19. 计算： $- 3^{2} + 2 \div \frac{2}{3} \times \frac{3}{2}$ ．
小虎同学的计算过程如下：原式 $= - 6 + 2 \div 1 = - 6 + 2 = - 4$

请你判断小虎的计算过程是否正确，若不正确，请你写出正确的计算过程．

查看试题解析
20. 下面的计算错在哪里？指出错误步骤的序号，并给出正确的解答过程.
$- 3^{2} \div （ - 2 ）^{3} \times （ - \frac{1}{8} ）$

$= 9 \div （ - 8) \times (- \frac{1}{8})$ ……①

$= 9 \div 1$ ……②

$= 9$ ……③

错误步骤的序号： ▲

正确解答：

查看试题解析
21. 若 $| x - 1 | + {(y + 2)}^{2} = 0$ ，求 $x - y$ 的值．

查看试题解析
22. 如图，一根细线上端固定，下端系一个小重物，让这个小重物来回自由摆动，来回摆动一次所用的时间 $t$ （单位： $s$ ）与细线的长度 $l$ （单位： $m$ ）之间满足关系 $t = 2 π \sqrt{\frac{l}{10}}$ ，当细线的长度为 $0 .5m$ 时，小重物来回摆动一次所用的时间是多少（结果保留小数点后一位）？（参考数据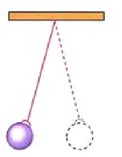： $\sqrt{5} \approx 2.24$ ， $π \approx 3.14$ ）

查看试题解析

五、综合题

23. 定义“*”运算：当a，b同号时，a*b＝＋（a²＋b²）；当a，b异号时，a*b＝﹣（a²﹣b²）．

(1)、求4*1的值．

(2)、求 $\frac{5}{2}$ *[（﹣2）*3]的值．

查看试题解析
24. 概念学习
规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2记作2₃ ，读作“2的3次商”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）₄ ，读作“﹣3的4次商”.一般地，我们把n个a（a≠0）相除记作a_n ，读作“a的n次商”.

(1)、初步探究
直接写出结果：2₃＝；

(2)、关于除方，下列说法错误的是；
①任何非零数的2次商都等于1；②对于任何正整数n，（﹣1）_n＝﹣1；③3₄＝4₃；④负数的奇数次商结果是负数，负数的偶数次商结果是正数.

(3)、深入思考
我们知道，有理数的减法运算可以转化为加法运算，除法运算能够转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？例： $2_{4} = 2 \div 2 \div 2 \div 2 = 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}$ .
试一试：仿照上面的算式，将下列运算结果直接写成乘方（幂）的形式（﹣3）₄＝； ${(\frac{1}{7})}_{5}$ ＝；

(4)、想一想：将一个非零有理数a的n次商写成幂的形式等于；

(5)、算一算： $5_{2} \div {(- \frac{1}{2})}_{4} \times {(- \frac{1}{3})}_{5} + {(- \frac{1}{4})}_{3} \times \frac{1}{4}$ ＝.

查看试题解析
25. 计算：

(1)、计算：12﹣(-6)+(﹣7)-15

(2)、计算：﹣5+（-12）-11-|﹣ $\frac{1}{2}$ |

(3)、计算：（-2）³+（-3）×[ ${(- \frac{1}{2})}^{2}$ ×4]÷（﹣2）

(4)、﹣1²⁰²¹+ $\frac{5}{2}$ ÷ $\frac{5}{8}$ ﹣ $\frac{2}{3}$ ×（﹣18）

(5)、观察下列各式：
- $1 \times \frac{1}{2}$ =-1+ $\frac{1}{2}$ ，- $\frac{1}{2} \times \frac{1}{3} =$ - $\frac{1}{2} + \frac{1}{3}$ ，- $\frac{1}{3} \times \frac{1}{4} =$ - $\frac{1}{3} + \frac{1}{4}$ ，……

①根据上述规律写出第5个等式是 ▲ ；

②规律应用：计算（- $1 \times \frac{1}{2}$ ）+（- $\frac{1}{2} \times \frac{1}{3}$ ）+（- $\frac{1}{3} \times \frac{1}{4}$ ）+…+（- $\frac{1}{2020} \times \frac{1}{2021}$ ）

③拓展应用：（直接写出结果）

$1 \times \frac{1}{3}$ + $\frac{1}{3} \times \frac{1}{5}$ + $\frac{1}{5} \times \frac{1}{7}$ +…+ $\frac{1}{2019} \times \frac{1}{2021}$ = ▲

查看试题解析
26. 已知10×10²＝1000＝10³ ，
10²×10²＝10000＝10⁴ ，

10²×10³＝100000＝10⁵.

(1)、猜想10⁶×10⁴＝， 10^m×10ⁿ＝.（m，n均为正整数）

(2)、运用上述猜想计算下列式子：
①（1.5×10⁴）×（1.2×10⁵）；

②（﹣6.4×10³）×（2×10⁶）.

查看试题解析