苏科版数学八年级上册2.5.5 等边三角形的性质和判定 同步训练
试卷更新日期：2021-12-18 类型：同步测试
一、单选题
-
1. 如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿BC方向平移2个单位后得到△DEF，连接DC，则DC的长为（ ）
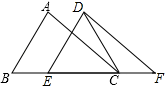A、3 B、4 C、5 D、62. 如图，在△ABE中，AE的垂直平分线MN交BE于点C，∠E＝30°，且AB＝CE，则∠BAE的度数是（ ）
A、80° B、85° C、90° D、105°3. 如图，正 的边长为4，过点 的直线 ，且 与 关于直线 对称， 为线段 上一动点，则 的最小值是（ ）.
A、 B、 C、8 D、4. 如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点．若 ，当 取得最小值时，则 的度数为（ ）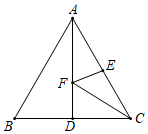
A、15° B、225° C、30° D、45°5. 如图所示，在 中， ， ， 于D ， 是 的平分线，且交 于P ， 如果 ，则AC的长为（ ）
A、1 B、2 C、3 D、46. 如图，在等边△ABC中，BD平分∠ABC交AC于点D，过点D作DE⊥BC于点E，且CE=2，则AB的长为（ ）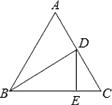
A、8 B、4 C、6 D、7.57. 如图，点P是∠AOB内任意一点，OP=6cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是6cm，则∠AOB的度数是（ ）
A、25° B、30° C、35° D、40°8.如图，正三角形ABC的三边表示三面镜子，BP=AB=1。一束光线从点P发射至BC上P1点，且∠BPP1=60。光线依次经BC反射，AC反射，AB反射…一直继续下去。当光线第一次回到点P时，这束光线所经过的路线的总长为（ ）
A、6 B、9 C、 D、279. 如图，P是等边△ABC内部一点，∠APB，∠BPC，∠CPA的大小之比是5：6：7，则以PA、PB、PC为边的三角形的三个内角的大小之比是（从小到大）（ ）
A、2：3：4 B、4：5：6 C、3：4：5 D、不确定10. 如图所示，已知△ABC和△BDE都是等边三角形，下列结论：①AE=CD；②BF=BG；③BH平分∠AHD；④∠AHC=60°；⑤△BFG是等边三角形；⑥FG∥AD，其中正确的有（ ）
A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 已知△ABC中，AB=AC=4，∠A=60°，则△ABC的周长为.
12. 如图，在△ABC中，AB＝BC＝2，∠BAC＝30°，分别以点A，C为圆心，AC的长为半径作弧，两弧交于点D，连接DA，DC，则四边形ABCD的面积为 ．
13. 如图，等边三角形纸片ABC的边长为6，E、F是边BC上的三等分点.分别过点E、F沿着平行于BA、CA方向各剪一刀，则剪下的△DEF的周长是.
14. 如图，∠AOB=30°，点M、N分别是射线OB、OA上的动点，点P为∠AOB内一点且OP=8，则△PMN的周长的最小值=。
15. 如图，在四边形ABCD中，AD＝BC ， ∠DAB＝50°，∠CBA＝70°，P、M、N分别是AB ， AC、BD的中点，若BC＝8，则△PMN的周长是 ．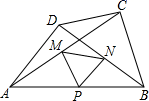
16. 如图，已知△ABC是等边三角形，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，有以下四个结论：①点P在∠BAC的平分线上；②△BRP≌△QSP；③QP∥AR；④△PQC是等边三角形，其中正确的有个.
17. 如图，在等边三角形ABC中，AD⊥BC，垂足为D，点P为AB边上一点，EF垂直平分线段BP，EF与线段AD交于F，连接CF、PF，以下结论：①PF＝CF；②∠PFC＝120°，③∠PFE+∠ACF＝90°；④∠PFA＝∠DCF．其中一定正确的有 ． （填序号即可）
三、解答题
-
18. 如图，在 中， ，点 为 边的中点， 于 ， .求 的长.
19. 边 中，点 是 边上的两个动点(不与点 重合)，点 在点 的左侧，且 ，点 关于直线 的的对称点为 ，连接 求证： ．
20. 如图，△ABC为等边三角形，∠BAD=∠ACF=∠CBE，求∠DEC的度数。
21. 如图， 是等边 外一点， 在 的延长线上，连接 ， ，且有 ， .求证： 为等边三角形.
22. 已知：等边△ABC，CE∥AB，D为BC上一点，且∠ADE=60°，求证：△ADE是等边三角形.
23. 如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ＝60°，且BP＝BQ，连结CQ．
(1)、观察并猜想AP与CQ之间的大小关系，并说明理由．(2)、若PA＝PC＝1，PB＝ ，求证：PC⊥CQ．24. 已知，如图，AB＝AD，∠B＝∠D，∠1＝∠2＝60°．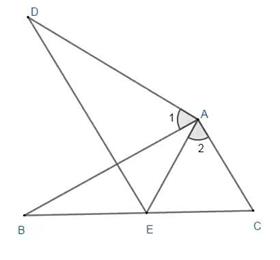
(1)、求证：△ADE≌△ABC；(2)、求证：AE＝CE．25. 如图，已知∠AOB＝60°，E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C，D是垂足，连接CD交OE于点F．
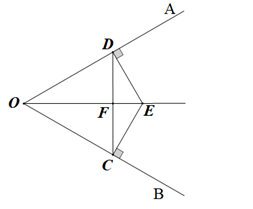(1)、求证：△OCD是等边三角形；(2)、若EF＝6，求线段OE的长．26. 如图，在 中， ， 为 的中点， 于点 ， 于点 ，且 ，连接 ，点 在 的延长线上，且 .
(1)、求证： 是等边三角形；(2)、若 ，求 的长.27. 如图， 是边长为 的等边三角形， 是 边上一动点，由 向 运动 与 ， 不重合 ， 是 延长线上一点，与点 同时以相同的速度由 向 延长线方向运动 不与 重合 ，过 作 于点 ，连接 交 于点 ．
(1)、若设AP=x，则PC= ， QC=；(用含x的式子表示)(2)、当∠BQD=30°时，求AP的长；(3)、在运动过程中线段DE的长是否发生变化？如果不变，求出线段DE的长；如果变化，请说明理由．28. 如图，已知△ABC和△DCE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F.
(1)、如图1，求证：∠1＝60°；(2)、如图2，连结FG，求∠2的度数；(3)、如图3，连结OC，若BD＝10，OC＝4，求△ACE的面积.