新疆昌吉州2021-2022学年高二上学期数学期中质量检测试卷

试卷更新日期：2021-12-17 类型：期中考试

进入出卷网下载

一、单选题

1. 袋内分别有红､白､黑球3，2，1个，从中任取2个，则互斥而不对立的两个事件是（）

A、至少有一个白球；都是白球 B、至少有一个白球；至少有一个红球 C、恰有一个白球；一个白球一个黑球 D、至少有一个白球；红､黑球各一个

查看试题解析
2. 如图，边长为2的正方形中有一阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为 $\frac{2}{3}$ .则阴影区域的面积约为 (　　)

A、 $\frac{2}{3}$ B、 $\frac{4}{3}$ C、 $\frac{8}{3}$ D、无法计算

查看试题解析
3. 命题“∀x∈R，x²﹣x+1≥0”的否定是（）

A、∀x∈R，x²﹣x+1＜0 B、∃x₀∈R，x₀²﹣x₀+1＜0 C、∃x₀∈R，x₀²﹣x₀+1≥0 D、∃x₀∈R，x₀²﹣x₀+1≤0

查看试题解析
4. “ $0 < m < 2$ ”是“方程 $\frac{x^{2}}{m} + \frac{y^{2}}{2 - m} = 1$ 表示椭圆”的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看试题解析
5. 点 $P (4, - 2)$ 与圆 $x^{2} + y^{2} = 4$ 上任一点连线的中点的轨迹方程是（）

A、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 1$ B、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 4$ C、 ${(x + 4)}^{2} + {(y - 2)}^{2} = 4$ D、 ${(x + 2)}^{2} + {(y - 1)}^{2} = 1$

查看试题解析
6. 已知 $F_{1}$ ， $F_{2}$ 是椭圆 $C$ 的两个焦点， $P$ 是 $C$ 上的一点，若 $P F_{1} ⊥ P F_{2}$ ，且 $∠ P F_{2} F_{1} = 60 °$ ，则 $C$ 的离心率为（）

A、 $1 - \frac{\sqrt{3}}{2}$ B、 $2 - \sqrt{3}$ C、 $\frac{\sqrt{3} - 1}{2}$ D、 $\sqrt{3} - 1$

查看试题解析
7. 下列说法正确的是（）

A、“若a＋b≥4，则a，b中至少有一个不小于2”的逆命题是真命题 B、命题“设a，b∈R，若a＋b≠6，则a≠3或b≠3”是一个真命题 C、“∃x₀∈R， ${x_{0}}^{2} - x_{0} < 0$ ”的否定是“∀x∈R，x²－x>0” D、“ $a + 1 > b$ ”是“ $a > b$ ”的一个充分不必要条件

查看试题解析
8. 某省在新的高考改革方案中规定：每位考生的高考成绩是按照3（语文、数学、英语） $+ 2$ （物理、历史）选 $1 + 4$ （化学、生物、地理、政治）选2的模式设置的，则某考生选择全理科的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{5}$ C、 $\frac{7}{10}$ D、 $\frac{1}{12}$

查看试题解析
9. 已知命题 $p ： | x - 1 | > 1$ ，命题 $q ： l n x \geq 1$ ，则 $p$ 是 $q$ 成立的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
10. 已知椭圆过点 $P (\frac{3}{5} ， - 4)$ 和点 $Q (- \frac{4}{5} ， - 3)$ ，则此椭圆的方程是（）

A、 $\frac{y^{2}}{25} + x^{2} = 1$ B、 $\frac{x^{2}}{25} + y^{2} = 1$ 或 $x^{2} + \frac{y^{2}}{25} = 1$ C、 $\frac{x^{2}}{25} + y^{2} = 1$ D、以上均不正确

查看试题解析
11. 设椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的两焦点为 $F_{1} ， F_{2}$ ，若椭圆上存在点 $P$ ，使 $∠ F_{1} P F_{2} = 120^{\circ}$ ，则椭圆的离心率 $e$ 的取值范围为（）.

A、 $(0 ， \frac{\sqrt{3}}{2}]$ B、 $(0 ， \frac{3}{4}]$ C、 $[\frac{\sqrt{3}}{2} ， 1)$ D、 $[\frac{3}{4} ， 1)$

查看试题解析
12. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的短轴长为2，上顶点为 $A$ ，左顶点为 $B$ ， $F_{1}$ ， $F_{2}$ 分别是 $C$ 的左、右焦点，且 $△ F_{1} A B$ 的面积为 $\frac{2 - \sqrt{3}}{2}$ ，点 $P$ 为 $C$ 上的任意一点，则 $\frac{1}{| P F_{1} |} + \frac{1}{| P F_{2} |}$ 的取值范围为（）

A、 $[1, 2]$ B、 $[\sqrt{2}, \sqrt{3}]$ C、 $[\sqrt{2}, 4]$ D、 $[1, 4]$

查看试题解析

二、填空题

13. 已知焦点在x轴上的椭圆 $\frac{x^{2}}{m} + y^{2} = 1 (m > 0)$ 的焦距为 $\sqrt{2}$ ，则m的值为．

查看试题解析
14. 从标有1，2，3，4，5的五张卡中，依次抽出2张，则在第一次抽到奇数的情况下，第二次抽到偶数的概率为；

查看试题解析
15. 命题p：（x﹣m）²＞3（x﹣m）是命题q：x²+3x﹣4＜0成立的必要不充分条件，则实数m的取值范围为.

查看试题解析
16. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，焦点F₁（-c，0）， F₂（c，0）（c> 0），若过F₁的直线和圆 $(x - \frac{1}{2} c)^{2} + y^{2} = c^{2}$ 相切，与椭圆在第一象限交于点P，且PF₂⊥x轴，则椭圆的离心率是.

查看试题解析

三、解答题

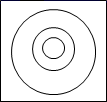
17. 如图在墙上挂着一块边长为 $16 c m$ 的正方形木板，上面画了小、中、大三个同心圆，半径分别为 $2 c m$ ， $4 c m$ ， $6 c m$ ，某人站在 $3 m$ 处向此木板投镖，设击中线上或没有投中木板时都不算，可重新投一次.
问：

(1)、投中大圆内的概率是多少？

(2)、投中小圆与中圆形成的圆环的概率是多少？

(3)、投中大圆且未投中小圆的概率是多少？

查看试题解析
18. 已知命题p： $\forall x \in R, a x^{2} + a x + 1 > 0$ ，命题 $q : | 2 a - 1 | < 3$ ．

(1)、若命题p是真命题，求实数a的取值范围；

(2)、若p∨q是真命题，p∧q是假命题，求实数a的取值范围．

查看试题解析
19. 20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：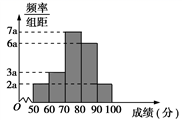

(1)、求频率直方图中a的值；

(2)、分别求出成绩落在[50，60)与[60，70)中的学生人数；

(3)、从成绩在[50，70)的学生中人选2人，求这2人的成绩都在[60，70)中的概率．

查看试题解析
20. 线段 $Q R$ 的长等于3，两端点 $Q$ ､ $R$ 分别在 $x$ 轴和 $y$ 轴上滑动，点 $S$ 在线段 $Q R$ 上，且 $\vec{R S} = 2 \vec{S Q}$ ，点 $S$ 的轨迹为曲线 $C$ .求曲线 $C$ 的方程.

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > 0, b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，短轴长为 $4$ ．

(1)、求椭圆的标准方程；

(2)、已知过点P（2,1）作弦且弦被P平分，则此弦所在的直线方程.

查看试题解析
22. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 的右焦点为 $(1, 0)$ ，且经过点 $A (0, 1)$ .
（Ⅰ）求椭圆C的方程；

（Ⅱ）设O为原点，直线 $l : y = k x + t (t \neq \pm 1)$ 与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，若|OM|·|ON|=2，求证：直线l经过定点.

查看试题解析