苏科版初中数学九年级上册2.1.1 圆的认识 同步训练
试卷更新日期:2021-12-17 类型:同步测试
一、单选题
-
1. 下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )A、1个 B、2个 C、3个 D、4个2. 下列说法正确的是( )A、弦是直径 B、平分弦的直径垂直于弦 C、优弧一定大于劣弧 D、等弧所对的圆心角相等3. 已知 的半径是6cm,则 中最长的弦长是( )A、6cm B、12cm C、16cm D、20cm4. 如图所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,点A与点B的距离是2 cm.若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出圆的直径是( )
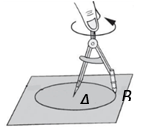 A、1 cm B、2 cm C、4 cm D、 cm5. 如图,以O为圆心的两个圆中,大圆的半径 分别交小圆于点C,D,连结 ,下列选项中不一定正确的是( )
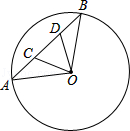
A、1 cm B、2 cm C、4 cm D、 cm5. 如图,以O为圆心的两个圆中,大圆的半径 分别交小圆于点C,D,连结 ,下列选项中不一定正确的是( )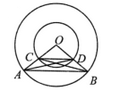 A、 B、 C、 D、6. 如图,不等边 内接于 ,下列结论不成立的是( )
A、 B、 C、 D、6. 如图,不等边 内接于 ,下列结论不成立的是( )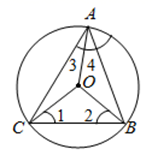 A、 B、 C、 D、7. 如图,点 、 、 在⊙O上, , ,则 的度数是( )
A、 B、 C、 D、7. 如图,点 、 、 在⊙O上, , ,则 的度数是( ) A、110° B、125° C、135° D、165°8. 如图,AC是⊙O的弦,AC=4,点B是⊙O上的一个动点,且∠ABC=45°,若点M,N分别是AC,BC的中点,则MN的最大值为( )
A、110° B、125° C、135° D、165°8. 如图,AC是⊙O的弦,AC=4,点B是⊙O上的一个动点,且∠ABC=45°,若点M,N分别是AC,BC的中点,则MN的最大值为( ) A、 B、4 C、6 D、9. 如图,在平面直角坐标系中, , , 半径为2,P为 上任意一点,E是PC的中点,则OE的最小值是( )
A、 B、4 C、6 D、9. 如图,在平面直角坐标系中, , , 半径为2,P为 上任意一点,E是PC的中点,则OE的最小值是( )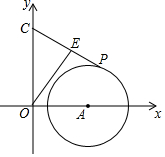 A、1 B、 C、2 D、10. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A、1 B、 C、2 D、10. 在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )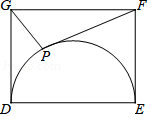 A、 B、
A、 B、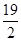 C、34
D、10
C、34
D、10
二、填空题
-
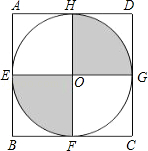
11. 在直径为10cm的⊙O中,弦AB=5cm,则∠AOB的度数为.12. 如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 .
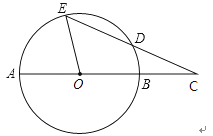
 13. 如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,则∠EOB的度数为.
13. 如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,则∠EOB的度数为.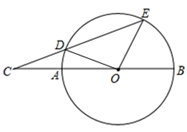 14. 如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则BC边的长为 .
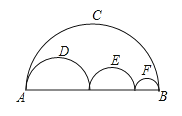
14. 如图,MN是⊙O的直径,矩形ABCD的顶点A、D在MN上,顶点B、C在⊙O上,若⊙O的半径为5,AB=4,则BC边的长为 . 15. 如图所示:点M、G、D在半圆O上,四边形OEDF、HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是bc(填<、=、>)
15. 如图所示:点M、G、D在半圆O上,四边形OEDF、HMNO均为矩形,EF=b,NH=c,则b与c之间的大小关系是bc(填<、=、>)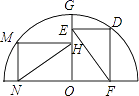 16. 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为cm.
16. 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为cm. 17. 如图,点M,N在半圆的直径AB上,点P,Q在 上,四边形MNPQ为正方形.若半圆的半径为 ,则正方形的边长为 .
17. 如图,点M,N在半圆的直径AB上,点P,Q在 上,四边形MNPQ为正方形.若半圆的半径为 ,则正方形的边长为 . 18. 过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为.
18. 过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为.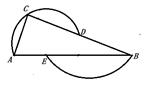
三、解答题
-
19. 如图,点O是线段AB的中点,根据要求完成下题:
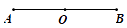 (1)、在图中补画完成:
(1)、在图中补画完成:第一步,以A B为直径的画出⊙O;
第二步,以B为圆心,以BO为半径画圆弧,交⊙O于点C,连接点CA,CO;
(2)、设AB=6,求扇形AOC的面积.(结果保留π)20. 已知:如图, 、 为 的半径, 、 分别为 、 的中点.求证: . 21. 已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
21. 已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.求证:△OAC≌△OBD.
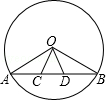 22. 已知:如图,在⊙O中,弦AB=CD.求证:∠AOC =∠BOD.
22. 已知:如图,在⊙O中,弦AB=CD.求证:∠AOC =∠BOD.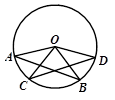 23. 已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
23. 已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.