高中数学人教A版（2019）选修一第三章圆锥曲线的方程

试卷更新日期：2021-12-17 类型：期末考试

进入出卷网下载

一、单选题

1. 椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 的长轴长为（）

A、4 B、8 C、6 D、18

查看试题解析
2. 椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{a^{2}} = 1$ 与双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{2} = 1$ 有相同的焦点，则实数a等于（）

A、 $\frac{1}{2}$ B、-1 C、1 D、-1或1

查看试题解析
3. 过双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的右焦点 $F$ 作双曲线渐近线的垂线段 $F M$ ，垂足为 $M$ ，线段 $F M$ 与双曲线交于点 $A$ ，且满足 $\vec{F A} = 2 \vec{A M}$ ，则双曲线离心率 $e$ 等于（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\frac{\sqrt{3} + 1}{2}$

查看试题解析
4. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，其左焦点F且斜率为 $\sqrt{3}$ 的直线与椭圆C相交于两点A，B，若 $\vec{A F} = 2 \vec{F B}$ ，则橢圆C的离心率为（）

A、 $\frac{2}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
5. 双曲线 $\frac{x^{2}}{25} - \frac{y^{2}}{24} = 1$ 的两个焦点为 $F_{1}$ ， $F_{2}$ ，双曲线上一点 $P$ 到 $F_{1}$ 的距离为11，则点 $P$ 到 $F_{2}$ 的距离为（）

A、1 B、21 C、1或21 D、2或21

查看试题解析
6. 已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ 的焦点F到其准线的距离为2，过点 $E （ 4 ， 0 ）$ 的直线l与抛物线C交于A，B两点，则 $| A F | + 2 | B F |$ 的最小值为（）

A、 $2 \sqrt{2} + 3$ B、 $8 \sqrt{2} + 3$ C、 $\frac{17}{8}$ D、9

查看试题解析
7. 已知抛物线 $y^{2} = 8 x$ 的焦点为F，经过点P(1，1)的直线l与该曲线交于A､B两点，且点P恰好为AB的中点，则 $| A F | + | B F | =$ （）

A、4 B、6 C、8 D、12

查看试题解析
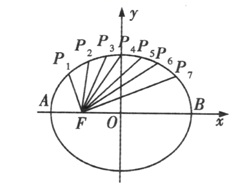8. 如图，把椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 的长轴 $A B$ 分成8等份，过每个分点作 $x$ 轴的垂线分别交椭圆的上半部分于点 $P_{1}$ ， $P_{2}$ ，…， $P_{7}$ ， $F$ 是左焦点，则 $| P_{1} F | + | P_{2} F | + \cdot \cdot \cdot + | P_{7} F | =$ （）

A、21 B、28 C、35 D、42

查看试题解析

二、多选题

9. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，直线 $l$ 与椭圆 $C$ 交于 $A$ ， $B$ 两点，直线 $y = - \frac{1}{2} x$ 与直线 $l$ 的交点恰好为线段 $A B$ 的中点，则（）

A、 $a = \sqrt{2} b$ B、 $a = 2 b$ C、直线 $l$ 的斜率为1 D、直线 $l$ 的斜率为4

查看试题解析
10. 已知椭圆 $C_{1} ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 与圆 $C_{2} ： x^{2} + y^{2} = b^{2}$ ，若在椭圆 $C_{1}$ 上存在点 $P$ ，使得由点 $P$ 所作的圆 $C_{2}$ 的两条切线相互垂直，则椭圆 $C_{1}$ 的离心率可以是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{4}{5}$

查看试题解析
11. 已知点 $P$ 是椭圆 $C ： \frac{x^{2}}{6} + y^{2} = 1$ 上的动点， $Q$ 是圆 $D ： {(x + 1)}^{2} + y^{2} = \frac{1}{5}$ 上的动点，点 $M (\frac{1}{2} ， \frac{1}{3})$ 则（）

A、椭圆 $C$ 的离心率为 $\frac{\sqrt{30}}{6}$ B、椭圆 $C$ 中以 $M$ 为中点的弦所在直线方程为 $6 x + 24 y - 11 = 0$ C、圆 $D$ 在椭圆 $C$ 的内部 D、 $P Q$ 的最小值为 $\frac{2 \sqrt{5}}{5}$

查看试题解析
12. 抛物线有如下光学性质：由其焦点射出的光线经抛物线反射后，沿平行于抛物线对称轴的方向射出；反之，平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点．已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ ，O为坐标原点，一条平行于x轴的光线 $l_{1}$ 从点 $P (\frac{41}{4} ， 4)$ 射入，经过C上的点A反射后，再经C上另一点B反射后，沿直线 $l_{2}$ 射出，经过点Q．下列说法正确的是（）

A、若 $p = 4$ ，则 $| A B | = 8$ B、若 $p = 2$ ，则 $| A B | = 8$ C、若 $p = 2$ ，则 $P B$ 平分 $∠ A B Q$ D、若 $p = 4$ ，延长 $A O$ 交直线 $x = - 2$ 于点M，则M，B，Q三点共线

查看试题解析

三、填空题

13. 如果方程 $k x^{2} + y^{2} = 2$ 表示焦点在y轴上的椭圆，那么实数k的取值范围是.

查看试题解析
14. 经过椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的左焦点 $F_{1}$ 作倾斜角为60º的直线 $l$ ，直线 $l$ 与椭圆相交于 $A ， B$ 两点，则线段 $A B$ 的长为．

查看试题解析
15. 椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - 4} = 1 (a > 2)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在椭圆 $C$ 上， $| O P | = 2$ （ $O$ 为坐标原点）， $S_{△ F_{1} P F_{2}} = 2$ ，则椭圆 $C$ 的长轴长为．

查看试题解析
16. 抛物线 $y^{2} = 8 x$ 的焦点为 $F$ ，点 $A (6 ， 3) ， P$ 为抛物线上一点，且 $P$ 不在直线 $A F$ 上，则 $Δ P A F$ 周长的最小值为．

查看试题解析

四、解答题

17. 设抛物线 $C ： y^{2} = 4 x$ 的焦点为 $F$ ，过 $F$ 的直线 $l$ 与 $C$ 交于 $A$ ， $B$ 两点．

(1)、若 $| A B | = 12$ ，求 $l$ 的方程．

(2)、以 $A$ ， $B$ 为切点分别作抛物线 $C$ 的两条切线，证明：两条切线的交点 $P$ 一定在定直线上，且 $P F ⊥ A B$ ．

查看试题解析
18. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率是 $\frac{1}{2}$ ，且点 $E (1 ， \frac{3}{2})$ 在椭圆 $C$ 上.

(1)、求椭圆 $C$ 的方程；

(2)、若过点 $P (0 ， 1)$ 的直线 $l$ 与椭圆 $C$ 相交于两个不同的点 $M$ 、 $N$ ，且 $| M N | = \frac{24}{7}$ ，求 $△ O M N$ （ $O$ 是坐标原点）的面积.

查看试题解析
19. 在直角坐标系 $x o y$ 中，椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）的左右焦点分别为 $F_{1}$ 和 $F_{2}$ ，若 $A$ 为椭圆上动点，直线 $A F_{2}$ 与椭圆交于另一点 $B$ ，若三角形 $A B F_{1}$ 的周长为为8，且点 $(1 ， - \frac{3}{2})$ 在椭圆上．

(1)、求椭圆的标准方程；

(2)、设直线 $F_{1} A$ 、 $F_{1} B$ 与直线 $x = 4$ 分别交于点 $M$ 、 $N$ ，记直线 $M F_{2}$ 和直线 $N F_{2}$ 的斜率分别为 $k_{1}$ 和 $k_{2}$ ，若 $k_{1} k_{2} = \frac{5}{4}$ ，试求直线 $A B$ 的斜率．

查看试题解析
20. 中心在原点，焦点在 $x$ 轴上的椭圆与双曲线有共同的焦点 $F_{1} 、 F_{2}$ ，且 $| F_{1} F_{2} | = 2 \sqrt{13}$ ，椭圆的长半轴长与双曲线的实半轴长之差为4，离心率之比为 $3 ： 7$ .

(1)、求椭圆和双曲线的方程；

(2)、若点 $Р$ 是椭圆和双曲线的一个交点，求 $c o s ∠ F_{1} P F_{2}$ .

查看试题解析
21. 在平面直角坐标系xOy中，如图，已知椭圆C： $\frac{x^{2}}{9}$ +y²=1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y=﹣3分别交于点M、N．

(1)、设直线AP、PB的斜率分别为k₁ ， k₂ ，求证：k₁•k₂为定值；

(2)、求线段MN长的最小值；

(3)、当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．

查看试题解析
22. 已知双曲线 $E$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的离心率为 $2$ ，点 $P (2 ， 3)$ 在 $E$ 上， $F$ 为 $E$ 的右焦点.

(1)、求双曲线 $E$ 的方程；

(2)、设 $Q$ 为 $E$ 的左顶点，过点 $F$ 作直线 $l$ 交 $E$ 于 $A ， B$ （ $A ， B$ 不与 $Q$ 重合）两点，点 $M$ 是 $A B$ 的中点，求证： $| A B | = 2 | M Q |$ .

查看试题解析

高中数学人教A版（2019） 选修一 第三章 圆锥曲线的方程

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教A版（2019）选修一第三章圆锥曲线的方程