苏科版数学八年级上册2.5.4 等边三角形的性质 同步训练
试卷更新日期:2021-12-16 类型:同步测试
一、单选题
-
1. 关于等腰三角形和等边三角形的区别与联系,下列说法中不正确的是( )A、有一个角是60°的等腰三角形是等边三角形 B、等边三角形是等腰三角形的特殊情况 C、等边三角形的底角与顶角相等 D、等边三角形包括等腰三角形2. 如图,在正方形 的外侧,作等边三角形 ,则 为( )
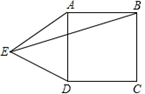 A、45° B、25° C、30° D、40°3. 如图,△ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC , 垂足为E , 延长BC到点Q , 使CQ=PA , 连接PQ交AC于点D , 则DE的长为( )
A、45° B、25° C、30° D、40°3. 如图,△ABC是边长为2的等边三角形,点P在AB上,过点P作PE⊥AC , 垂足为E , 延长BC到点Q , 使CQ=PA , 连接PQ交AC于点D , 则DE的长为( ) A、0.5 B、0.9 C、1 D、1.254. 等边△ABC中,AB=7,DE绕点D逆时针转过60°,E点落在BC边的F处,已知AE=2,则BF=( )
A、0.5 B、0.9 C、1 D、1.254. 等边△ABC中,AB=7,DE绕点D逆时针转过60°,E点落在BC边的F处,已知AE=2,则BF=( )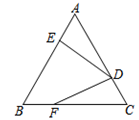 A、2 B、3 C、3.5 D、55. 如图,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( )
A、2 B、3 C、3.5 D、55. 如图,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( ) A、5 B、10 C、15 D、206. 如图所示,ΔABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )
A、5 B、10 C、15 D、206. 如图所示,ΔABC是等边三角形,且BD=CE,∠1=15°,则∠2的度数为( )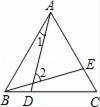 A、15° B、40° C、45° D、60°7. 已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其正确的个数有( )个
A、15° B、40° C、45° D、60°7. 已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其正确的个数有( )个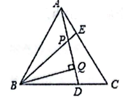 A、1 B、2 C、3 D、48. 如图,已知 ,点 , , ,…,在射线 上,点 , , , ,…,在射线 上, , , ,…,均为等边三角形.若 ,则 的边长为( )
A、1 B、2 C、3 D、48. 如图,已知 ,点 , , ,…,在射线 上,点 , , , ,…,在射线 上, , , ,…,均为等边三角形.若 ,则 的边长为( ) A、 B、 C、 D、9. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;② CM=CN;③ AC=DN.其中,正确结论的个数是 ( )
A、 B、 C、 D、9. 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;② CM=CN;③ AC=DN.其中,正确结论的个数是 ( ) A、3个 B、2个 C、1个 D、0个10. 如图所示,已知 和 均是等边三角形,点B、C、E在同一条直线上,连接 、 、 , 与 交于点O, 与 交于点G, 与 交于点F,则下列结论中:
A、3个 B、2个 C、1个 D、0个10. 如图所示,已知 和 均是等边三角形,点B、C、E在同一条直线上,连接 、 、 , 与 交于点O, 与 交于点G, 与 交于点F,则下列结论中:① ; ② ; ③ ; ④ ,以上结论正确的有( )
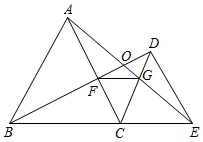 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
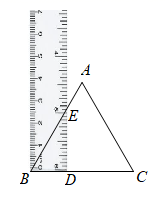
11. 小明在纸上面了一个边长为5cm的等边三角形 ,并将一个宽为2cm直尺如图所示放在所画 上,使得直尺一条边与 的边BC重合,另一条边交边AB于点E , 则AE= .
 12. 如图, 是等边 的 边上的中点,点 在 的延长线上, , 的周长是9,则 .
12. 如图, 是等边 的 边上的中点,点 在 的延长线上, , 的周长是9,则 . 13. 如图,△ABC是等边三角形,∠CBD=90°,BD=BC , 连接AD交BC于点E , 则∠AEC的度数是 .
13. 如图,△ABC是等边三角形,∠CBD=90°,BD=BC , 连接AD交BC于点E , 则∠AEC的度数是 . 14. 如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD= .
14. 如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD= .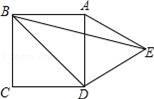 15. 如图,过边长为3的等边△ABC的边AB上一点P , 作PE⊥AC于E , Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D , 则DE的长为 .
15. 如图,过边长为3的等边△ABC的边AB上一点P , 作PE⊥AC于E , Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D , 则DE的长为 . 16. 如图,已知:等边三角形ABC , 点D是AB的中点,过点D作DF⊥AC , 垂足为F , 过点F作FE⊥BC , 垂足为E , 若三角形ABC的边长为4.则线段BE的长为 .
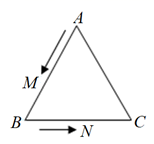
16. 如图,已知:等边三角形ABC , 点D是AB的中点,过点D作DF⊥AC , 垂足为F , 过点F作FE⊥BC , 垂足为E , 若三角形ABC的边长为4.则线段BE的长为 . 17. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是
17. 如图,已知等边△ABC的边长为8cm,∠A=∠B=60°,点D为边BC上一点,且BD=3cm.若点M在线段CA上以2cm/s的速度由点C向点A运动,同时,点N在线段AB上由点A向点B运动,△CDM与△AMN全等,则点N的运动速度是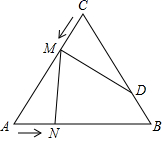 18. 如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有(填序号即可).
18. 如图所示,△ABC为等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,有下列四个结论:①点P在∠BAC的平分线上;②AS=AR;③QP∥AB;④△BRP≌△CSP.其中,正确的有(填序号即可).
三、解答题
-
19. 如图,已知等边 分别在 上,且 ,连接 交 点.求证:
 20. 如图:△ABC和△CDE是等边三角形.求证:BE=AD.
20. 如图:△ABC和△CDE是等边三角形.求证:BE=AD. 21. 如图所示: 是等边三角形, 、 分别是 及 延长线上的一点,且 ,连接 交 于点 .
21. 如图所示: 是等边三角形, 、 分别是 及 延长线上的一点,且 ,连接 交 于点 .

求证:
22. 如图, 是边长为1的等边三角形, , ,点 , 分别在 , 上,且 ,求 的周长.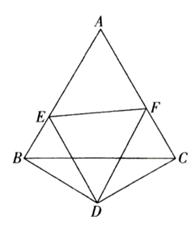 23. 已知:如图,B、C、D在同一直线上,△ABC,△ADE是等边三角形,求证:CE=AB+CD.
23. 已知:如图,B、C、D在同一直线上,△ABC,△ADE是等边三角形,求证:CE=AB+CD.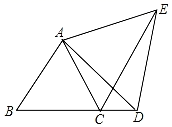 24. 已知, 和 都是等边三角形,且点B,C,D在同一条直线上.求证:BE=AD.
24. 已知, 和 都是等边三角形,且点B,C,D在同一条直线上.求证:BE=AD. 25. 如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G.求证:AD=PE+PF+PG.
25. 如图,点P是等边三角形ABC内一点,AD⊥BC于点D,PE⊥AB于点E,PF⊥AC于点F,PG⊥BC于点G.求证:AD=PE+PF+PG.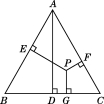 26. 如图, 与 都是等边三角形,连结 .
26. 如图, 与 都是等边三角形,连结 .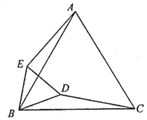 (1)、求证: ;(2)、连结 ,若 ,求 的长.
(1)、求证: ;(2)、连结 ,若 ,求 的长.