苏科版数学八年级上册2.5.3 等腰三角形的判定和性质 同步训练
试卷更新日期:2021-12-16 类型:同步测试
一、单选题
-
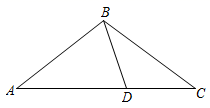
1. 如图, 中,点 在 上,连接BD,∠ABD=2∠DBC,∠ADB=2∠C,∠DBC=∠A,则图中共有等腰三角形( )
 A、0个 B、1个 C、2个 D、3个2. 如图,在△ABC 中,∠ABC 的平分线交 AC 于点 D,AD=6,过点 D 作 DE∥BC 交 AB 于点 E, 若△AED 的周长为 16,则边 AB 的长为( )
A、0个 B、1个 C、2个 D、3个2. 如图,在△ABC 中,∠ABC 的平分线交 AC 于点 D,AD=6,过点 D 作 DE∥BC 交 AB 于点 E, 若△AED 的周长为 16,则边 AB 的长为( )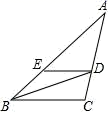 A、6 B、8 C、10 D、13. 如图,CE平分∠BCD且CE⊥BD于点E,∠DAB=∠ABD,AC=24,△BCD的周长为34,则BD的长为( )
A、6 B、8 C、10 D、13. 如图,CE平分∠BCD且CE⊥BD于点E,∠DAB=∠ABD,AC=24,△BCD的周长为34,则BD的长为( )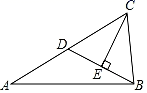 A、10 B、12 C、14 D、164. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
A、10 B、12 C、14 D、164. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )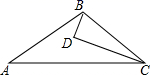 A、1 B、 C、 D、45. 如图, 中, , 平分 ,以下结论:
A、1 B、 C、 D、45. 如图, 中, , 平分 ,以下结论:①线段 是线段 的垂直平分线② 是等腰三角形;③ ;④ 为 的中点.其中正确的有( )
 A、1个 B、2个 C、3个 D、4个6. 如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是( )
A、1个 B、2个 C、3个 D、4个6. 如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是( )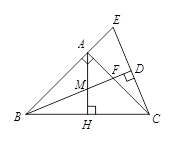 A、∠E=67.5 B、∠AMF=∠AFM C、BF=2CD D、BD=AB+AF7. 如图,在 △ABC 中,ED∥BC , ∠ABC 和∠ACB 的平分线分别交 ED 于点 G 、F , 若 FG = 2 ,ED = 6 ,则EB + DC 的值为( )
A、∠E=67.5 B、∠AMF=∠AFM C、BF=2CD D、BD=AB+AF7. 如图,在 △ABC 中,ED∥BC , ∠ABC 和∠ACB 的平分线分别交 ED 于点 G 、F , 若 FG = 2 ,ED = 6 ,则EB + DC 的值为( )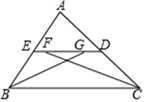 A、6 B、7 C、8 D、98. 如图, 中, 是 的角平分线, 的垂直平分线分别交 于点 ,则下列结论不一定成立的是( )
A、6 B、7 C、8 D、98. 如图, 中, 是 的角平分线, 的垂直平分线分别交 于点 ,则下列结论不一定成立的是( ) A、 B、 C、 D、9. 如图所示,在 中, , 是 的角平分线, , ,垂足分别为E、F,① , ;② ;③若点P为 上任意一点,且 ,则 的取值范围是 ;④ .其中,正确的个数是( )
A、 B、 C、 D、9. 如图所示,在 中, , 是 的角平分线, , ,垂足分别为E、F,① , ;② ;③若点P为 上任意一点,且 ,则 的取值范围是 ;④ .其中,正确的个数是( )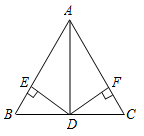 A、1个 B、2个 C、3个 D、4个10. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠AEB=180°;③∠ACE=∠EBC;④AD=AE;其中正确的结论有( )个
A、1个 B、2个 C、3个 D、4个10. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠AEB=180°;③∠ACE=∠EBC;④AD=AE;其中正确的结论有( )个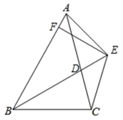 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
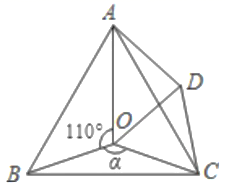
11. 在△ABC中,若∠A = 100°,∠B = 40°,AC = 5,则AB = .12. 如图, 和 相交于点 ,且 , , ,则 .
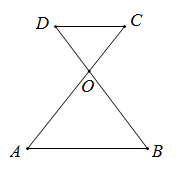 13. 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=7cm,DE=3cm,求CE的长为cm.
13. 如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,若BD=7cm,DE=3cm,求CE的长为cm.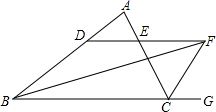 14. 如图,在 中, , , 是线段 的垂直平分线,连接 ,若 , ,则用含有a,b的代数式表示 的周长是.
14. 如图,在 中, , , 是线段 的垂直平分线,连接 ,若 , ,则用含有a,b的代数式表示 的周长是.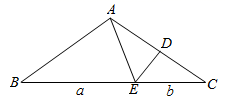 15. 如图,△ABC的周长为26,点D、 E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是.
15. 如图,△ABC的周长为26,点D、 E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P.若BC=10,则PQ的长是.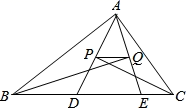 16. 如图,将一张长方形纸片ABCD按图中方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是.
16. 如图,将一张长方形纸片ABCD按图中方式进行折叠,若AE=3,AB=4,BE=5,则重叠部分的面积是.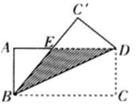 17. 已知:如图,△ABC中,E在BC上,D在BA上,过E作EF⊥AB于F,∠B=∠1+∠2,AE=CD,BF 则AD的长为.
17. 已知:如图,△ABC中,E在BC上,D在BA上,过E作EF⊥AB于F,∠B=∠1+∠2,AE=CD,BF 则AD的长为.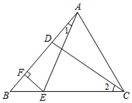 18. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .
18. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .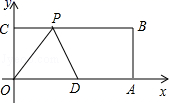
三、解答题
-
19. 如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F,FD∥AC交BC于点D.求证:△AEF是等腰三角形.
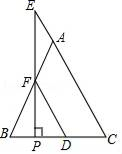 20. 如图,已知D是∠ABC的平分线与△ABC的外角平分线的交点,DE∥BC,交AB于点E,交AC于点F.
20. 如图,已知D是∠ABC的平分线与△ABC的外角平分线的交点,DE∥BC,交AB于点E,交AC于点F.求证:EF=BE-CF
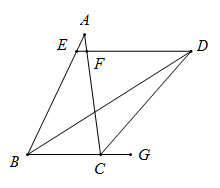 21. 如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.
21. 如图,在四边形ABCD中,AD=BC,E,F,G,H分别是AB,CD,AC,EF的中点,求证:GH⊥EF.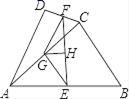 22. 如图,D为∠ACB平分线上一点,DE⊥CA于E,DF⊥CB于F.试探究CD与EF的位置关系,并证明你的结论.
22. 如图,D为∠ACB平分线上一点,DE⊥CA于E,DF⊥CB于F.试探究CD与EF的位置关系,并证明你的结论.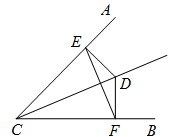 23. 如图,在 中, , 于 , 的平分线 交 于点 ,交 于 , 于 .求证: .
23. 如图,在 中, , 于 , 的平分线 交 于点 ,交 于 , 于 .求证: .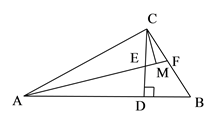 24. 如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证:
24. 如图,在△ABC中,D,E分别是AB,AC边上的点,且∠1=∠2,CD=BE.CD与BE相交于点O.求证: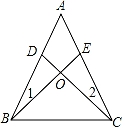 (1)、AB=AC.(2)、OB=OC.25. 如图,BD和AD分别平分△ABC的内角∠CBA和外角∠CAG,BD交AC于F.
(1)、AB=AC.(2)、OB=OC.25. 如图,BD和AD分别平分△ABC的内角∠CBA和外角∠CAG,BD交AC于F.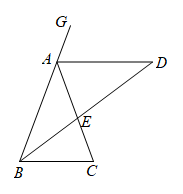 (1)、若AB=AC,请判断△ABD的形状,并证明你的结论;(2)、在(1)的条件下,若AE=BE,求∠ABC的大小.
(1)、若AB=AC,请判断△ABD的形状,并证明你的结论;(2)、在(1)的条件下,若AE=BE,求∠ABC的大小.