山西省运城市盐湖区2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在 $△$ BCD中，CD边上的高是（）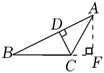

A、BD B、AD C、AF D、CD

查看试题解析
3. 如图， $△$ ABC≌ $△$ DEC ， B ， C ， D三点在同一直线上，若CE=6，AC=9，则BD的长为（）

A、3 B、9 C、12 D、15

查看试题解析
4. 已知三角形三个内角的度数之比为3：3：4，则这个三角形是（）

A、等腰三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
5. 如图，在正五边形ABCDE中，连接AD ，则∠DAE的度数为（）

A、46° B、56° C、36° D、26°

查看试题解析
6. 如图 $△$ ABC≌ $△ A^{'} B^{'} C^{'}$ ，边 $B^{'} C^{'}$ 过点A且平分∠BAC交BC于点D ， ∠B=26°， $∠ C D B^{'}$ =94°，则 $∠ C^{'}$ 的度数为（）

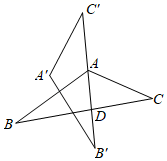A、34° B、40° C、45° D、60°

查看试题解析
7. 如图，在 $△$ ABC中，AD平分∠BAC ， $D E // A C$ ，AB=7cm，BD=3cm，则 $△$ BDE的周长为（）

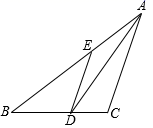A、13cm B、10cm C、4cm D、7cm

查看试题解析
8. 如图，在 $△$ ABC中，∠ABC的平分线BP与AC的垂直平分线DP相交于点P ，过点P作PF⊥BC于点F ， PE⊥AB交BA的延长线于点E ． AB=7cm，BC=15cm，则AE的长为（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
9. 如图，点D在AC上，点B在AE上， $△$ ABC≌ $△$ DBE ．若∠A：∠C=5：3，则∠DBC的度数为（）

A、12° B、24° C、20° D、36°

查看试题解析
10. 有一题目：“如图，∠ABC=40°，BD平分∠ABC ，过点D作DE∥AB交BC于点E ，若点F在AB上，且满足DF=DE ，求∠DFB的度数．”小贤的解答：以D为圆心，DE长为半径画圆交AB于点F ，连接DF ，则DE=DF ，由图形的对称性可得∠DFB=∠DEB ．结合平行线的性质可求得∠DFB=140°．而小军说：“小贤考虑的不周全，∠DFB还应有另一个不同的值”．下列判断正确的是（）

A、小军说的对，且∠DFB的另一个值是40° B、小军说的不对，∠DFB只有140°一个值 C、小贤求的结果不对，∠DFB应该是20° D、两人都不对，∠DFB应有3个不同值

查看试题解析

二、填空题

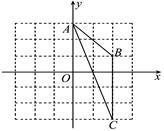
11. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是．

查看试题解析
12. 如图，已知A(0，3)，B(2，1)，C(2，－3)，若点P是△ABC三边垂直平分线的交点，则点P的坐标为．

查看试题解析
13. 如图， $△$ ABC的周长为30cm，把 $△$ ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连接AD，若AE=4cm，则 $△$ ABD的周长是．

查看试题解析
14. 如图，已知△ABC的周长是20，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝2，△ABC的面积是．

查看试题解析
15. 有一个三角形纸片 $A B C$ ， $∠ C = 30 °$ ，点D是 $A C$ 边上一点，沿 $B D$ 方向剪开三角形纸片后，发现所得的两纸片均为等腰三角形，则 $∠ A$ 的度数可以是．

查看试题解析

三、解答题

16.

(1)、如图1，在 $△$ ABC中，∠B=40°，∠C=60°，AD⊥BC于点D ， AE是∠BAC的平分线，求∠DAE的度数．

(2)、如图2，点E ， F在BC上，BE=CF ， AB=DC ， ∠B=∠C ．求证：∠A=∠D ．

查看试题解析
17. 如图，四边形 $A B C D$ 中， $A B = A C$ ， $∠ B = ∠ C$ ，求证： $B D = C D$ .

查看试题解析
18. 如图，在 $△$ ABC中，AB=AC ， ∠BAC=90°，点A在直线l上，BM⊥，CN⊥l ，垂足分别为M ， N ．

(1)、你能找到一对全等的三角形吗？并说明理由．

(2)、线段BM ， CN ， MN之间有何数量关系？并说明理由．

查看试题解析
19. 如图，在等腰 $△$ ABC中，AB=AC=6cm，∠B=30°，点D在BC边上由点C向点B匀速运动（点D不与点B ， C重合），速度为2cm/s，连接AD ，作∠ADE=30°，DE交线段AC于点E ．

(1)、在此运动过程中，∠BDA逐渐变（填“大”或“小”）；D点运动到图1位置时，∠BDA=75°，则∠BAD=°．

(2)、点D运动3s后到达图2位置，则CD=cm．此时 $△$ ABD和 $△$ DCE是否全等，请说明理由．

(3)、在点D运动过程中， $△$ ADE的形状也在变化．当 $△$ ADE是等腰三角形时，∠BDA的度数为．

查看试题解析
20. 如图，在平面直角坐标系中，A(-1，3)，B(-1，-2)，C(-4，1)．

(1)、求 $△$ ABC的面积．

(2)、在图中作出 $△$ ABC关于y轴的对称图形 $△$ A₁B₁C₁ ．

(3)、写出点A₁ ， B₁ ， C₁的坐标．

查看试题解析
21. 如图，点 $C$ 在线段 $A B$ 上， $A D // E B$ ， $A C = B E$ ， $A D = B C$ ，点 $F$ 是 $D E$ 的中点.

求证：

(1)、 $△ A C D ≌ △ B E C$ ；

(2)、 $C F ⊥ D E$ .

查看试题解析
22. 如图，将 $△$ ABC分别沿AB ， AC翻折得到 $△$ ABD和 $△$ AEC ，线段BD与AE交于点F ，连接BE ．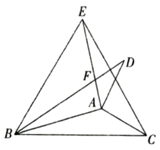

(1)、若∠ABC=20°，∠ACB=30°，求∠DAE及∠BFE的度数．

(2)、若BD所在的直线与CE所在的直线互相垂直，求∠CAB的度数．

查看试题解析
23. 定义：顶角相等且顶点重合的两个等腰三角形叫做对顶三角形．如图1，在 $△$ OAB与 $△$ OCD中，OA=OB ， OC=OD ， ∠AOB=∠COD ．

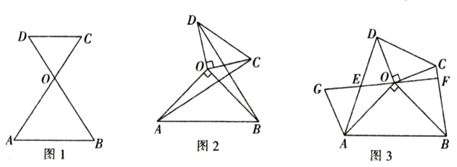(1)、如图1， $△$ OAB与 $△$ OCD是对顶三角形，且A ， O ， C三点共线请判断AB与CD的位置关系，并说明理由．

(2)、如图2， $△$ OAB与 $△$ OCD是对顶三角形，∠AOB=∠COD=90°，连接AC ， BD ，试探究线段AC ， BD之间的关系，并说明理由．

(3)、如图3， $△$ OAB与 $△$ OCD是对顶三角形，∠AOB=∠COD=90°，连接AD ， BC ，取AD的中点E ，连接EO并延长交BC于点F ，延长OE至点G ，使EG=OE ，连接AG ，求证：EF⊥BC ．

查看试题解析