山东省枣庄市峄城区2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 一个长方形抽屉长 $3 cm$ ，宽 $4 cm$ ，贴抽屉底面放一根木棒，那么这根木棒最长（不计木棒粗细）可以是（）

A、 $4 cm$ B、 $5 cm$ C、 $6 cm$ D、 $7 cm$

查看试题解析
2. 下列四组数中，是勾股数的是（　　）

A、5，12，13 B、4，5，6 C、2，3，4 D、1， $\sqrt{2}$ ， $\sqrt{3}$

查看试题解析
3. 《九章算术》是我国古代数学的经典著作，书中有一个“折竹抵地”问题：“今有竹高丈，末折抵地，问折者高几何？”意思是：一根竹子，原来高一丈（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？（　　）

A、4尺 B、4.55尺 C、5尺 D、5.55尺

查看试题解析
4. 数轴上A ， B ， C ， D四点中，两点之间的距离最接近于 $\sqrt{6}$ 的是（　　）

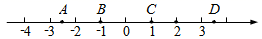A、点C和点D B、点B和点C C、点A和点C D、点A和点B

查看试题解析
5. 下列计算正确的是（）．

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt[3]{9} = 3$ C、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ D、 ${(- \sqrt{3})}^{0} = 1$

查看试题解析
6. 下列说法中，错误的是（）．

A、4的算术平方根是2 B、8的立方根是 $\pm 2$ C、 $\sqrt{81}$ 的平方根是 $\pm 3$ D、立方根等于－1的实数是－1

查看试题解析
7. 如图，点A，B都在格点上，若 $B C= \frac{2 \sqrt{13}}{3}$ ，则 $A C$ 的长为（）

A、 $\sqrt{13}$ B、 $\frac{4 \sqrt{13}}{3}$ C、 $2 \sqrt{13}$ D、 $3 \sqrt{13}$

查看试题解析
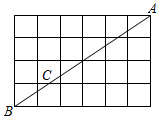8. 根据下列表述，不能确定具体位置的是（）

A、教室内的3排4列 B、渠江镇胜利街道15号 C、南偏西 $30 °$ D、东经 $108 °$ ，北纬 $53 °$

查看试题解析
9. 在平面直角坐标系 $x O y$ 中，点 $M (- 4, 2)$ 关于x轴对称的点的坐标是（）

A、 $(- 4, 2)$ B、 $(4, 2)$ C、 $(- 4, - 2)$ D、 $(4, - 2)$

查看试题解析
10. 某物体在力F的作用下，沿力的方向移动的距离为S，力对物体所做的功W与S的对应关系如图所示，则下列结论正确的是（）

A、 $W = \frac{1}{8} S$ B、 $W = 20 S$ C、 $W = 8 S$ D、 $S = \frac{160}{W}$

查看试题解析
11. 如图，直线y=ax+b过点A（0，2）和点B（﹣3，0），则方程ax+b=0的解是（）

A、x=2 B、x=0 C、x=﹣1 D、x=﹣3

查看试题解析
12. 甲、乙两人沿同一条路从A地出发，去往100千米外的B地，甲、乙两人离A地的距离（千米）与时间t（小时）之间的关系如图所示，以下说法正确的是（）

A、甲的速度是 $60km/h$ B、乙的速度是 $30km/h$ C、乙同时到达 D、甲出发两小时后两人第一次相遇

查看试题解析

二、填空题

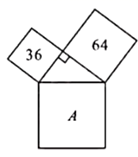
13. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为.

查看试题解析
14. 在 $0 ， \frac{22}{7} ， - 0.101001 ， π ， \sqrt[3]{8}$ 中无理数的个数是个．

查看试题解析
15. 如图，长方体的长为15，宽为10，高为20，点B离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是．

查看试题解析
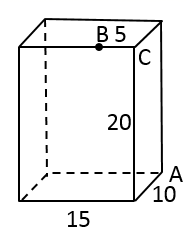16. 在平面直角坐标系中，点M在第四象限，且点M到y轴的距离是3，到x轴的距离是1，则点M的坐标是．

查看试题解析
17. 在正比例函数 $y = k x$ 中，y的值随着x值的增大而增大，则点 $P (3 ， k)$ 在第象限.

查看试题解析
18. 某市为提倡居民节约用水，自今年1月1日起调整居民用水价格．图中 $l_{1}$ 、 $l_{2}$ 分别表示去年、今年水费y（元）与用水量x（ $m^{3}$ ）之间的关系．小雨家去年用水量为150 $m^{3}$ ，若今年用水量与去年相同，水费将比去年多元．

查看试题解析

三、解答题

19. 解下列各题：

(1)、计算： $\sqrt[3]{- 27} + \sqrt{5} (\sqrt{5} - \frac{1}{\sqrt{5}})$ ；

(2)、计算： $| \sqrt{3} | + {(\sqrt{3} - \frac{1}{2})}^{2} - {(\sqrt{3} + \frac{1}{2})}^{2}$ ；

(3)、如图，点A是数轴上表示实数a的点．

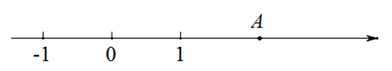
①用直尺和圆规在数轴上作出表示实数的 $\sqrt{2}$ 的点P；（保留作图痕迹，不写作法）

②利用数轴比较 $\sqrt{2}$ 和a的大小，并说明理由．

查看试题解析
20. 解下列各题：
已知 $△ A B C$ 在如图所示的平面直角坐标系中．

(1)、直接写出三个顶点的坐标：A ， B ， C（）

(2)、将A、B、C三点的横坐标保持不变，纵坐标分别乘－1，得到点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，在图中描出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，并画出 $△ A_{1} B_{1} C_{1}$ ；

(3)、图中的 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 的位置关系为；

(4)、求 $△ A B C$ 的面积．

查看试题解析
21. 有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m的一棵大树上，大树高14m ，且巢离树顶部1m ．当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s ，那它至少需要多少时间才能赶回巢中？

查看试题解析
22. 设一个三角形的三边长分别为a、b、c ， $P = \frac{1}{2} (a + b + c)$ ，则有下列面积公式：
$S = \sqrt{P (P - a) (P - b) (P - c)}$ （海伦公式）．

(1)、一个三角形边长依次为5、6、7，利用海伦公式求这个三角形的面积；

(2)、一个三角形边长依次为2、 $\sqrt{6}$ 、3，利用海伦公式求这个三角形的面积．

查看试题解析
23. 某农贸公司销售一批玉米种子，若一次购买不超过5千克，则种子价格为20元/千克，若一次购买超过5千克，则超过5千克部分的种子价格打8折．设一次购买量为x千克，付款金额为y元．

(1)、求y关于x函数解析式；

(2)、某农户一次购买玉米种子30千克，需付款多少元？

查看试题解析
24. 某某鲜花销售公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成．

如图中的射线l₁ ，射线l₂分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资y₁（单位：元）和y₂（单位：元）与其当月鲜花销售量x（单位：千克）（x≥0）的函数关系．分别求y₁、y₂与x的函数解析式（解析式也称表达式）．

查看试题解析