山东省济南市长清区2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 16的平方根是（）

A、8 B、±8 C、±4 D、4

查看试题解析
2. 在平面直角坐标系中，点（0，﹣2）在（　　）

A、x轴上 B、y轴上 C、第三象限 D、第四象限

查看试题解析
3. 下列二次根式中，是最简二次根式的是（　　）

A、 $\sqrt{20}$ B、 $\sqrt{30}$ C、 $\sqrt{40}$ D、 $\sqrt{50}$

查看试题解析
4. 平面直角坐标系内，点P（-3，-4）到y轴的距离是（）

A、3 B、4 C、5 D、-3或7

查看试题解析
5. 函数 y=2x-1的图象不经过的点是（　　）

A、（1，1） B、（2，3） C、（﹣1，﹣1） D、（﹣2，﹣5）

查看试题解析
6. 已知 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ 是方程x﹣my＝3的解，那么m的值为（　　）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
7. 下列各式中，正确的是（　　）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ B、 $\sqrt{27} \div \sqrt{3} = 9$ C、 $(\sqrt{5} + 1) (\sqrt{5} - 1) = 4$ D、 ${(\sqrt{3} + \sqrt{2})}^{2} = 5$

查看试题解析
8. 如图，点 $A 、 B 、 C$ 都在方格纸的格点上，若点A的坐标为 $(0 ， 2)$ ，点B的坐标为 $(2 ， 0)$ ，则点C的坐标是（）

A、 $(2 ， 2)$ B、 $(1 ， 2)$ C、 $(1 ， 1)$ D、 $(2 ， 1)$

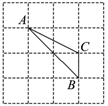查看试题解析
9. 某校举行篮球赛，每场比赛都要分出胜负，每队胜一场得2分，负一场得1分．八年级一班在16场比赛中得26分，设该班胜x场，负y场，则根据题意，下列方程组中正确的是（　　）

A、 ${\begin{matrix} x + y = 16 \\ 2 x + y = 26 \end{matrix}$ B、 ${\begin{matrix} x + y = 26 \\ 2 x + y = 16 \end{matrix}$ C、 ${\begin{matrix} x + y = 16 \\ x + 2 y = 26 \end{matrix}$ D、 ${\begin{matrix} x + y = 26 \\ x + 2 y = 16 \end{matrix}$

查看试题解析
10. 正比例函数y＝kx（k≠0）的函数值y随x的增大而增大，则一次函数y＝x﹣k的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
11. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为（）

A、23cm B、24cm C、25cm D、26cm

查看试题解析
12. 东东和爸爸一起出去运动，两人同时从家出发，沿相同路线前行，途中爸爸有事返回，东东继续前行，5分钟后也原路返回，两人恰好同时到家．东东和爸爸在整个运动过程中离家的路程y₁（米），y₂（米）与运动时间x（分）之间的函数关系如图所示，下列结论中正确的是（　　）
①两人前行过程中的速度为200米/分；

②m的值是15，n的值是3000；

③东东开始返回时与爸爸相距1500米；

④运动18分钟或30分钟时，两人相距900米．

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

13. 计算： $\sqrt{4}$ +（﹣1）²＝．

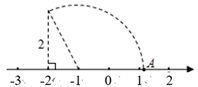
查看试题解析
14. 在平面直角坐标系中，将点P（﹣1，2）向右平移3个单位得到点Q ，则点Q的坐标为．

查看试题解析
15. 若点A（1，y₁），B（3，y₂）在一次函数y＝﹣x+b的图象上，则y₁y₂（填“＞”“＜”或“＝”）．

查看试题解析
16. 已知关于x、y的二元一次方程组 ${\begin{matrix} 2 x + y = a \\ x - y = 1 \end{matrix}$ 的解为 ${\begin{matrix} x = 3 \\ y = b \end{matrix}$ ，则a+b的值为．

查看试题解析
17. 如图，在数轴上点A表示的实数是 .

查看试题解析
18. 平面直角坐标系xOy中，点A₁ ， A₂ ， A₃ ， ……和B₁ ， B₂ ， B₃ ， ……分别在直线y＝ $\frac{1}{3}$ x+ $\frac{2}{3}$ 和x轴上，△OA₁B₁ ， △B₁A₂B₂ ， △B₂A₃B₃ ， ……都是等腰直角三角形，如果A₁（1，1），则点A₂₀₂₁的纵坐标是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}}$ ；

(2)、（ $\sqrt{13}$ +3）（ $\sqrt{13}$ ﹣3）．

查看试题解析
20. 计算：

(1)、（ $\sqrt{12} - \sqrt{\frac{1}{3}}$ ）× $\sqrt{3}$ ；

(2)、（ $\sqrt{24} - \sqrt{6} + \sqrt{5}$ ）² ．

查看试题解析
21. 解方程组 ${\begin{matrix} x - y = 3 \\ 2 x - 3 y = 8 \end{matrix}$ ．

查看试题解析
22. 如图所示的方格纸中，每个小方格的边长都是1，点A（﹣4，1）、B（﹣3，3）、C（﹣1，2）．

⑴作△ABC关于y轴对称的△A'B'C'；

⑵在x轴上找出点P ，使PA+PC最小，在图中描出满足条件的P点（保留作图痕迹），并直接写出P点的坐标．

查看试题解析
23. 某手机专营店代理销售A、B两种型号手机．手机的进价、售价如表：

型号

A

B

进价

1200元/部

1000元/部

售价

1380元/部

1200元/部

用36000元购进A、B两种型号的手机，全部售完后获利6300元，求购进A、B两种型号手机的数量．

查看试题解析
24. 观察下列一组等式，解答后面的问题：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2}$ ﹣1，

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$

应用计算：

(1)、利用上面的方法进行化简： $\frac{1}{\sqrt{7} + \sqrt{6}}$ ；

(2)、归纳：根据上面的结论，找规律，请直接写出下列算式的结果： $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝；

(3)、拓展： $\frac{1}{\sqrt{101} + \sqrt{100}} + \frac{1}{\sqrt{102} + \sqrt{101}} + \frac{1}{\sqrt{103} + \sqrt{102}} + \dots \dots + \frac{1}{\sqrt{2021} + \sqrt{2020}}$ ＝．

查看试题解析
25. 如图，直线l是一次函数y＝kx+b的图象，直线经过点（3，﹣3），交x轴于点A ，交y轴于点B（0，1）．

(1)、求直线l的解析式；

(2)、求l与两坐标轴所围成的三角形的面积；

(3)、当x时，y≥0；

(4)、求原点到直线l的距离．

查看试题解析
26. 如图1，小刚家，学校、图书馆在同一条直线上，小刚骑自行车匀速从学校到图书馆，到达图书馆还完书后，再以相同的速度原路返回家中（上、下车时间忽略不计）．小刚离家的距离 $y (m)$ 与他所用的时间 $x (min)$ 的函数关系如图2所示．

(1)、小刚家与学校的距离为m，小刚骑自行车的速度为 $m/min$ ；

(2)、求小刚从图书馆返回家的过程中，y与x的函数表达式；

(3)、小刚出发35分钟时，他离家有多远?

查看试题解析
27. 在平面直角坐标系中，长方形OABC的边OA在x轴上，OC在y轴上，B（4，3），点M从点A开始，以每秒1个单位长度的速度沿AB→BC→CO运动，设△AOM的面积为S ，点M运动的时间为t ．

(1)、当0＜t＜3时，AM=；当7＜t＜10时，OM= ．（用含t的代数式表示）

(2)、当7＜t＜10时，求S关于t的函数关系式；

(3)、当t=8时，在x轴上是否存在一点H ，使得△MBH是以MB为直角边的直角三角形，若存在，请求出点H的坐标；若不存在，请说明理由．

查看试题解析

型号	A	B
进价	1200元/部	1000元/部
售价	1380元/部	1200元/部