山东省菏泽市东明县2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（　　）

A、3；4；5 B、3；4；6 C、9；12；15 D、4； $\frac{15}{2}$ ； $\frac{17}{2}$

查看试题解析
2. 在实数 $\sqrt{5}$ ， $\frac{π}{2}$ ， $\frac{22}{7}$ ，2.1313313331…（每两个1之间依次多1个3）中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列二次根式属于最简二次根式的是（）

A、 $\sqrt{2 x^{2}}$ B、 $\sqrt{125}$ C、 $\sqrt{26}$ D、 $\sqrt{0.01}$

查看试题解析
4. 若点B(m+1，3m﹣5)到x轴的距离与到y轴的距离相等，则点B的坐标是（）

A、(4，4)或(2，2) B、(4，4)或(2，﹣2) C、(2，﹣2) D、(4，4)

查看试题解析
5. 下列说法正确的是（）

A、（﹣2）²的平方根是﹣2 B、4是 $\sqrt{16}$ 的算术平方根 C、 $\sqrt{4}$ 的平方根是 $\pm \sqrt{2}$ D、 $\sqrt{3}$ 是 $\pm \sqrt{9}$ 的算术平方根

查看试题解析
6. 如图，在2×2的网格中，有一个格点△ABC，若每个小正方形的边长为1，则△ABC的边AB上的高为（）

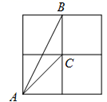A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{5}}{10}$ D、1

查看试题解析
7. 关于一次函数y＝﹣x﹣3，下列结论正确的是（）

A、图象过点(﹣1，1) B、图象在y轴上的截距为3 C、y随x的增大而增大 D、图象经过第二、三、四象限

查看试题解析
8. 已知点A(﹣3，y₁)和B(﹣2，y₂)都在直线y＝﹣ $\frac{1}{2}$ x﹣b上，则y₁ ， y₂的大小关系是（）

A、y₁＞y₂ B、y₁＜y₂ C、y₁＝y₂ D、大小不确定

查看试题解析
9. 下列条件中，不能判断一个三角形是直角三角形的是（）

A、三个角的度数比为1：2：3 B、三条边的长度比为1：2：3 C、三条边满足关系a²+c²=b² D、三个角满足关系∠B+∠C=∠A

查看试题解析
10. 一次函数y＝kx－k(k＜0)的图象大致是(　　)

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若（2x﹣5）²+ $\sqrt{4 y + 1}$ ＝0，则2x+4y的平方根是．

查看试题解析
12. 已知 $△$ ABC中∠C＝90°，c为斜边，a、b为直角边，若a+b＝17cm ， c＝13cm ，则 $△$ ABC的面积为．

查看试题解析
13. 已知实数a，b，c在数轴上的位置如图所示，化简代数式 $\sqrt{a^{2}} - | a + c | + \sqrt{{(b - c)}^{2}} - | - b |$

查看试题解析
14. 函数 $y = (m + 3) x^{m^{2} - 8} - 5$ 是一次函数，则 $m =$ .

查看试题解析
15. ﹣8的立方根是， 4的平方根是．

查看试题解析
16. 如图所示的圆柱体中底面圆的周长是2，高为3，若一只小虫从A点出发沿着圆柱体的侧面匀速爬行一周到B点，则小虫爬行的最短路程是．

查看试题解析

三、解答题

17. 计算：

(1)、2 $\sqrt{18}$ ﹣6× $\sqrt{\frac{1}{2}} + \sqrt[3]{- 27}$ ；

(2)、（ $\sqrt{5}$ ﹣2）²﹣（ $\sqrt{13}$ ﹣2）（ $\sqrt{13}$ +2）；

(3)、（1+ $\sqrt{3}$ ）•（2﹣ $\sqrt{3}$ ）；

(4)、 $\frac{3 - \sqrt{3}}{\sqrt{3}} - \frac{2 - \sqrt{2}}{\sqrt{2}}$ ．

查看试题解析
18. 如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米每秒的速度收绳，10秒后船移动到点D的位置，问船向岸边移动了多少米？（假设绳子是直的，结果保留根号）

查看试题解析
19. A、B两地相距300千米，甲、乙两车先后从A地出发到B地．如图，线段OC表示甲车离A地距离y（千米）与时间x（小时）之间的函数关系；折线DEF表示乙车离A地距离y（千米）与x（小时）之间的函数关系．根据图象回答下列问题．

(1)、求线段EF对应的函数解析式；

(2)、乙车到达B地后，甲车距B地多少千米？

(3)、求点P的坐标，并说出点P坐标的实际意义．

查看试题解析
20. 已知（x﹣5+ $\sqrt{3}$ ）²+ $\sqrt{y - 5 - \sqrt{3}}$ ＝0．

(1)、求x ， y的值．

(2)、求xy的算术平方根．

查看试题解析
21. 已知y与3x﹣2成正比例，且当x＝2时，y＝8．

(1)、求y与x的函数关系式；

(2)、求当x＝﹣2时的函数值；

(3)、如果y与x的函数图象与x轴相交于点A ，图象与y轴相交于点B ，求 $△$ AOB的面积．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，△ABC的位置如图所示．

(1)、分别写出△ABC各个顶点的坐标．

(2)、请在图中画出△ABC关于y轴对称的图形△A'B'C'．

(3)、计算出△ABC的面积．

查看试题解析
23. 已知：如图1，OA＝2，∠A＝90°， $O C ∥ A B$ ，OB平分∠AOC ，且CB⊥OB于点B ．

(1)、求OC的长；

(2)、将图1的四边形ABCO折叠，如图2，使点C与点A重合，折痕为FG ，求OG的长．

查看试题解析