山东省菏泽市曹县2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-12-16 类型:期中考试
一、单选题
-
1. 若分式 有意义,则x的取值范围是( )A、x≠2 B、x≠﹣2 C、x≠4 D、x≠﹣42. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,点D在AB上.点E在AC上,AB=AC . 增加下列一个条件后,仍不能判定△ABE≌△ACD的是( )
3. 如图,点D在AB上.点E在AC上,AB=AC . 增加下列一个条件后,仍不能判定△ABE≌△ACD的是( ) A、∠AEB=∠ADC B、∠B=∠C C、AE=AD D、BE=CD4. 计算 的结果是( )A、 B、 C、 D、5. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( )
A、∠AEB=∠ADC B、∠B=∠C C、AE=AD D、BE=CD4. 计算 的结果是( )A、 B、 C、 D、5. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( ) A、3cm B、4cm C、6cm D、8cm6. 计算 的结果是( )A、 B、 C、 D、7. 已知点P(3,2x﹣4)关于x轴的对称点在第一象限,则x的取值范围是( )A、x>2 B、x<2 C、x>0 D、x<08. 如图,AD , BE分别是△ABC的中线和角平分线,AB=AC , ∠CAD=20°,则∠ABE的度数为( )
A、3cm B、4cm C、6cm D、8cm6. 计算 的结果是( )A、 B、 C、 D、7. 已知点P(3,2x﹣4)关于x轴的对称点在第一象限,则x的取值范围是( )A、x>2 B、x<2 C、x>0 D、x<08. 如图,AD , BE分别是△ABC的中线和角平分线,AB=AC , ∠CAD=20°,则∠ABE的度数为( ) A、20° B、35° C、40° D、70°9. 如图,正方形的网格中,点A , B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )
A、20° B、35° C、40° D、70°9. 如图,正方形的网格中,点A , B是小正方形的顶点,如果C点是小正方形的顶点,且使△ABC是等腰三角形,则点C的个数为( )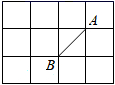 A、6 B、7 C、8 D、910. 如图,AD=BC , AE=CF . E、F是BD上两点,BE=DF , ∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A、6 B、7 C、8 D、910. 如图,AD=BC , AE=CF . E、F是BD上两点,BE=DF , ∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )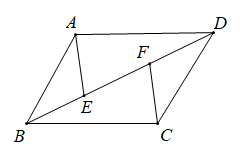 A、30° B、60° C、70° D、80°
A、30° B、60° C、70° D、80°二、填空题
-
11. 计算( )2• 的结果是 .12. 如图,点D与点D'关于AE对称,∠CED'=60°,则∠AED的度数为 .
 13. 化简分式 的结果是 .14. 如图,AC平分∠DAB , 要使△ABC≌△ADC , 需要增加的一个条件是 .
13. 化简分式 的结果是 .14. 如图,AC平分∠DAB , 要使△ABC≌△ADC , 需要增加的一个条件是 .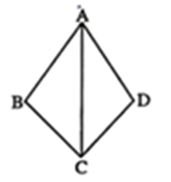 15. 如图,在 中, ,边 的垂直平分线 交 于点D, 平分 ,则 .
15. 如图,在 中, ,边 的垂直平分线 交 于点D, 平分 ,则 . 16. 计算 的结果是 .17. 如图,△ABC是等边三角形,AD⊥BC于点D , AE=AD , 则∠ADE的度数为 .
16. 计算 的结果是 .17. 如图,△ABC是等边三角形,AD⊥BC于点D , AE=AD , 则∠ADE的度数为 . 18. 如图,四边形ABCD中,AD BC , ∠A=90°,AD=4cm , BD=BC=7cm , CE⊥BD于点E , 则DE的长cm .
18. 如图,四边形ABCD中,AD BC , ∠A=90°,AD=4cm , BD=BC=7cm , CE⊥BD于点E , 则DE的长cm .
三、解答题
-
19. 计算:(1)、 ;(2)、 ;(3)、 .20. 先化简,再求值: ,其中x= .21. 已知四边形OABC , O为坐标原点,点A、B、C的坐标分别为A(﹣2,﹣4),B(4,﹣3),C(3,0),在如图所示的平面直角坐标系中画出四边形OABC和它关于y轴对称的四边形OA′B′C′,并分别写出点A , B , C的对应点A′,B′,C′的坐标.
 22. 如图,已知线段a和∠α,求作△ABC , 使AB=a , ∠A= ∠α,∠B=∠α(使用直尺和圆规,并保留作图痕迹).
22. 如图,已知线段a和∠α,求作△ABC , 使AB=a , ∠A= ∠α,∠B=∠α(使用直尺和圆规,并保留作图痕迹). 23. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数.
23. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数. 24. 如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.
24. 如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:△ABC≌△CED.


