山东省德州市2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-12-16 类型:期中考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算错误的是( )A、x3•x4=x7 B、(x2)3=x6 C、x3÷x3=x D、(﹣2xy2)4=16x4y83. 我国的纸伞工艺十分巧妙,如图,伞圈 D 能沿着伞柄滑动,伞不论张开还是缩拢,伞柄 AP 始终平分同一平面内所成的角∠BAC,为了证明这个结论,我们的依据是( )
2. 下列计算错误的是( )A、x3•x4=x7 B、(x2)3=x6 C、x3÷x3=x D、(﹣2xy2)4=16x4y83. 我国的纸伞工艺十分巧妙,如图,伞圈 D 能沿着伞柄滑动,伞不论张开还是缩拢,伞柄 AP 始终平分同一平面内所成的角∠BAC,为了证明这个结论,我们的依据是( ) A、SAS B、SSS C、AAS D、ASA4. 如果代数式(x﹣2)(x2+mx+1)的展开式不含x2项,那么m的值为( )A、2 B、 C、-2 D、5. 如图所示,在下列条件中,不能判断 ≌ 的条件是( )
A、SAS B、SSS C、AAS D、ASA4. 如果代数式(x﹣2)(x2+mx+1)的展开式不含x2项,那么m的值为( )A、2 B、 C、-2 D、5. 如图所示,在下列条件中,不能判断 ≌ 的条件是( ) A、 , B、 , C、 , D、 ,6. 下列命题中正确的有( )个
A、 , B、 , C、 , D、 ,6. 下列命题中正确的有( )个⑴有两个角互余的三角形是直角三角形;(2)有一个角等于60°的等腰三角形是等边三角形;(3)等腰三角形的角平分线、中线、高互相重合;(4)在角的内部,到角的两边距离相等的点在这个角的平分线上.
A、1 B、2 C、3 D、47. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )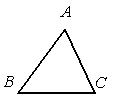 A、
A、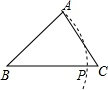 B、
B、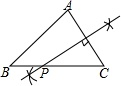 C、
C、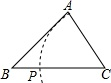 D、
D、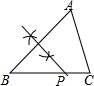 8. 如图, 是 的角平分线, ,垂足为F, , 和 的面积分别为29和16,则 的面积为( )
8. 如图, 是 的角平分线, ,垂足为F, , 和 的面积分别为29和16,则 的面积为( ) A、13 B、6.5 C、11 D、5.59. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°10. 已知a=255 , b=344 , c=433 , 则a , b , c的大小关系是( )A、b>c>a B、a>b>c C、c>a>b D、a>c>b11. 如图,已知△ABC中,AB=AC=24cm,∠B=∠C , BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等.
A、13 B、6.5 C、11 D、5.59. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°10. 已知a=255 , b=344 , c=433 , 则a , b , c的大小关系是( )A、b>c>a B、a>b>c C、c>a>b D、a>c>b11. 如图,已知△ABC中,AB=AC=24cm,∠B=∠C , BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等. A、4 B、3 C、4或3 D、4或612. 如图,在 直角△ABC中, ,AB=AC , 点D为BC中点,直角 绕点D旋转,DM , DN分别与边AB , AC交于E , F两点,下列结论:①△DEF是等腰直角三角形;② AE=CF;③△BDE≌△ADF;④ BE+CF=EF , 其中正确结论是( )
A、4 B、3 C、4或3 D、4或612. 如图,在 直角△ABC中, ,AB=AC , 点D为BC中点,直角 绕点D旋转,DM , DN分别与边AB , AC交于E , F两点,下列结论:①△DEF是等腰直角三角形;② AE=CF;③△BDE≌△ADF;④ BE+CF=EF , 其中正确结论是( )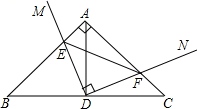 A、①②④ B、②③④ C、①②③ D、①②③④
A、①②④ B、②③④ C、①②③ D、①②③④二、填空题
-
13. 已知点A(x , ﹣4)与点B(3,y)关于x轴对称,那么x+y的值为 .14. (﹣2)2021+(﹣2)2020= .15. 如图,在△ABC中,AB和AC的垂直平分线分别交BC于E、F,若∠BAC=130°,则∠EAF= .
 16. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm.
16. 王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为cm. 17. 如图1,若在边长为a的正方形硬纸板的四角各剪掉一个矩形(图1中阴影部分,其中有两个小正方形),将剩余部分按图中的线条折成一个有盖的长方体盒子(图2).若剪掉的一个小正方形的边长为b , 此时长方体盒子表面积是 .
17. 如图1,若在边长为a的正方形硬纸板的四角各剪掉一个矩形(图1中阴影部分,其中有两个小正方形),将剩余部分按图中的线条折成一个有盖的长方体盒子(图2).若剪掉的一个小正方形的边长为b , 此时长方体盒子表面积是 . 18. 如图,△ABC中,AB=AC,BC=5, ,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,最这个最小值为
18. 如图,△ABC中,AB=AC,BC=5, ,AD⊥BC于点D,EF垂直平分AB,交AC于点F,在EF上确定一点P,使PB+PD最小,最这个最小值为
三、解答题
-
19.(1)、计算:﹣(﹣x)2(﹣2x2y)3+2x2(x6y3﹣1)(x2+1)0;(2)、已知2x+5y﹣3=0,求4x•32y的值.20. 先化简,再求值:[(﹣2y)2﹣(2x﹣y)(3x+y)﹣5y2]÷( x),其中,x、y满足|x﹣1|+(y+3)2=0.21. 如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:

⑴画出△ABC关于x轴的对称图形ΔA1B1C1;直接写出A1、B1、C1的坐标;
⑵如图,在直线l上找一点M , 使得AM+BM的值最小.(保留作图痕迹)
22. 如图,△ABC中,∠C=90°.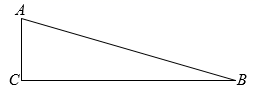 (1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .23. 如图,△ABC是等边三角形,点D、E分别在边BC、AC上,AE=CD , AD与BE相交于点F , BG⊥AD , 垂足为G .
(1)、求作△AEB , 使△AEB是以AB为底的等腰三角形,且使点E在边BC上.(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图形中,若∠CAE:∠EAB=4:1,求∠AEB的度数;(3)、在(2)的条件下,求证:BE=2AC .23. 如图,△ABC是等边三角形,点D、E分别在边BC、AC上,AE=CD , AD与BE相交于点F , BG⊥AD , 垂足为G . (1)、求证:△ABE≌△CAD;(2)、若FG=3,EF=1,求AD的长.24. 一般地,n个相同的因数a相乘a•a•…•a , 记为an;如2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).(1)、计算下列各对数的值:log24=;log216=;log264=;(2)、你能得到log24、log216、log264之间满足怎样的关系式:;(3)、由(2)的结果,请你归纳出logaM、logaN、logaMN之间满足的关系式:;(4)、根据幂的运算以及对数的含义验证(3)的结论.25. 某中学八年级学生在学习等腰三角形的相关知识时时,经历了以下学习过程:
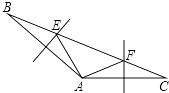
(1)、求证:△ABE≌△CAD;(2)、若FG=3,EF=1,求AD的长.24. 一般地,n个相同的因数a相乘a•a•…•a , 记为an;如2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).(1)、计算下列各对数的值:log24=;log216=;log264=;(2)、你能得到log24、log216、log264之间满足怎样的关系式:;(3)、由(2)的结果,请你归纳出logaM、logaN、logaMN之间满足的关系式:;(4)、根据幂的运算以及对数的含义验证(3)的结论.25. 某中学八年级学生在学习等腰三角形的相关知识时时,经历了以下学习过程: (1)、(探究发现)如图1,在 中,若 平分 , 时,可以得出 ,D为 中点,请用所学知识证明此结论.(2)、(学以致用)如果 和等腰 有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且 ,试探究线段 和 的数量关系,并证明.(3)、(拓展应用)如图3,在(2)的前提下,若顶点C与顶点F不重合, ,(2)中的结论还成立吗?证明你的结论
(1)、(探究发现)如图1,在 中,若 平分 , 时,可以得出 ,D为 中点,请用所学知识证明此结论.(2)、(学以致用)如果 和等腰 有一个公共的顶点B,如图2,若顶点C与顶点F也重合,且 ,试探究线段 和 的数量关系,并证明.(3)、(拓展应用)如图3,在(2)的前提下,若顶点C与顶点F不重合, ,(2)中的结论还成立吗?证明你的结论