山东省滨州市博兴县2021-2022学年八年级上学期数学期中试卷
试卷更新日期：2021-12-16 类型：期中考试
一、单选题
-
1. 下列图形：线段、角、正方形、圆，其中是轴对称图形个数的为（ ）A、1 B、2 C、3 D、42. 下列长度的三条线段首尾顺次相接，能够组成三角形的是（ ）A、3，5，10 B、5，7，12 C、4，4，8 D、8，8，103. 在钝角△ABC中，若其三条边上的高所在直线相交于点O ， 则点O在△ABC的（ ）A、内部 B、外部 C、边上 D、无法确定4. 下列说法：①全等三角形是指面积相等的三角形，②周长相等的三角形是全等三角形，③全等三角形是指形状相同大小相等的三角形，④所有的等边三角形都是全等三角形，其中正确的个数为（ ）A、1 B、2 C、3 D、45. 若点P（﹣2，3）关于y轴的对称点为Q（a ， b），则点为Q坐标为（ ）A、（﹣2，﹣3） B、（2，3） C、（2，﹣3） D、（﹣2，3）6. 在△ABC中，若∠A＝45°，∠B＝50°，则△ABC是（ ）A、锐角三角形 B、直角三角形 C、等边三角形 D、钝角三角形7. 如图，点A、D、C、F在同一条直线上，若AB＝DE ， BC＝EF ， 则下列条件中能满足△ABC≌△DEF的是（ ）
A、∠A＝∠EDF B、AD＝CF C、∠BCA＝∠F D、BC EF8. 如图，AD是△ABC的角平分线，DE⊥AB于点E ， S△ABC=10，DE=2，AB=4， 则AC长是（ ）
A、9 B、8 C、7 D、69. 等腰三角形一腰上的高与另一腰的夹角为20°，则其底角的大小为（ ）A、65° B、105° C、55°或35° D、65°或115°10. 如图，Rt△ABC中，∠C＝90°，∠B＝60°．首先以顶点B为圆心、适当长为半径作弧，在边BC、BA上截取BE、BD；然后分别以点D、E为圆心、以大于 的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G ． 若BG＝1，P为边AB上一动点，则GP的最小值为（ ）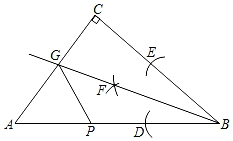
A、无法确定 B、 C、1 D、211. 如图，若点O是△ABC内一点且∠BOC＝140°，∠1＝20°，∠2＝40°，则∠A的大小为（ ）
A、80° B、100° C、120° D、无法确定12. 如图，△ABC≌△AED ， 点E在线段BC上，∠1＝44°，则∠AED的大小为（ ）
A、70° B、68° C、64° D、62°二、填空题
-
13. 七边形的内角和是14. 如图，点D在△ABC边BC的延长线上，CE平分∠ACD ， ∠A＝80°，∠B＝30°，则∠ACE的大小为 ．
15. 等腰三角形的一边长为4cm，周长为14cm，则该三角形的底边长为 ．16. 如图，已知：∠A＝∠D，∠1＝∠2，下列条件中：①∠E＝∠B；②EF＝ BC；③AB＝ EF；④AF＝CD．能使△ABC≌△DEF的有；(填序号)
17. 如图，Rt△AOB≌Rt△CDA ， 且点A、B的坐标分别为（﹣1，0），b（0，2），则点D的坐标是 ．
18. 如图，AD平分∠BAC ， DE AB ， DF⊥AB ． 若AE＝8，∠BAC＝30°，则DF的长为 ．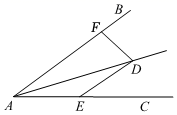
三、解答题
-
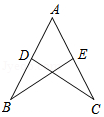
19. 在△ABC中，若∠A﹣∠B﹣∠C＝20°，求∠A的大小．20. 如图，点D在AB上，点E在AC上，AB＝AC，BD＝CE，求证：∠B＝∠C．
21. 如图，已知△ABC各顶点坐标分别为A（﹣3，2）、B（﹣4，﹣3）、C（﹣1，﹣1）．
(1)、画出△ABC关于x轴对称的△A1B1C1；(2)、写出△ABC关于y轴对称的△A2B2C2的各顶点坐标．
