辽宁省锦州市北镇市2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，无理数是（　　）

A、 $\sqrt{9}$ B、π C、﹣ $\frac{1}{3}$ D、5

查看试题解析
2. 已知点A的坐标为（﹣4，﹣3），则点A在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 分别以下列四组线段为三边，能构成直角三角形的是（　　）

A、0.3，0.4，0.5 B、1，1，2 C、1，2，3 D、9，16，25

查看试题解析
4. 若y＝mx^|m﹣1|是正比例函数，则m的值是（　　）

A、0 B、1 C、2 D、0或﹣2

查看试题解析
5. 估计 $\sqrt{5} + 1$ 的值在（）

A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间

查看试题解析
6. 如图所示，在正方形网格中有A ， B ， C三个点，若建立平面直角坐标系后，点A的坐标为（2，1），点B的坐标为（1，﹣2），则点C的坐标为（　　）

A、（1，1） B、（﹣2，1） C、（﹣1，﹣2） D、（﹣2，﹣1）

查看试题解析
7. 如图，有一个圆柱，它的高等于12cm，底面上圆的周长等于18cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，则蚂蚁沿圆柱侧面爬行的最短路程是（　　）

A、15cm B、17cm C、18cm D、30cm

查看试题解析
8. 在正比例函数y＝kx中，y的值随着x值的增大而减小，则一次函数y＝kx+k在平面直角坐标系中的图象大致是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

9. $27$ 的立方根是．

查看试题解析
10. 如果一个数的平方根是2x+1和x﹣7，那么这个数是．

查看试题解析
11. 已知点A（﹣2，y₁），B（3，y₂）在一次函数y＝2x﹣3的图象上，则y₁y₂（填“＞”，“＜”或“＝”）．

查看试题解析
12. 长方形ABCD在平面直角坐标系中的位置如图所示，若AD＝5，点B的坐标为（﹣3，3），则点C的坐标为．

查看试题解析
13. 如图，在△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD⊥AB于点D ，则CD的长为．

查看试题解析
14. 若实数x ， y满足y＝3 $\sqrt{x - 5}$ +2 $\sqrt{5 - x}$ +8，则2x﹣y＝．

查看试题解析
15. 如图，正方形ABCD是由9个边长为1的小正方形组成的，点E ， F均在格点（每个小正方形的顶点都是格点）上，连接AE ， AF ，则∠EAF的度数是．

查看试题解析
16. 如图，在平面直角坐标系xOy中，点A₁ ， A₂ ， A₃ ， …分别在x轴上，点B₁ ， B₂ ， B₃ ， …分别在直线y＝x上，△OA₁B₁ ， △B₁A₁A₂ ， △B₁B₂A₂ ， △B₂A₂A₃ ， △B₂B₃A₃…，都是等腰直角三角形，如果OA₁＝1，则点A₂₀₁₉的坐标为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{8}$ ﹣（π﹣3.14）⁰+| $\sqrt{2}$ ﹣2|

(2)、 $\sqrt{18}$ ﹣4 $\sqrt{\frac{1}{8}}$ ﹣2（ $\sqrt{2}$ ﹣1）

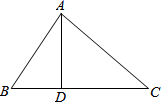
(3)、（2 $\sqrt{5} - \sqrt{7}$ ）（2 $\sqrt{5} + \sqrt{7}$ ）﹣（ $\sqrt{5}$ ﹣3）²

查看试题解析
18. 如图，在△ABC中，D是BC边上的一点，若AB＝5，BD＝3，AD＝4，AC＝8，求CD的长．

查看试题解析
19. 在弹性限度内，弹簧的长度与所挂物体质量满足一次函数关系，某数学兴趣小组通过实验发现弹簧的长度y（cm）与所挂物体质量x（kg）之间的关系如下表：

x/kg

0

1

2

3

⋯

y/cm

14.5

15

15.5

16

⋯

(1)、根据上表数据求出y与x之间的关系式；

(2)、求当所挂物体的质量为6千克时弹簧的长度．

查看试题解析
20. 如图，在平面直角坐标中，△ABC各顶点都在小方格的格点上．

⑴画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出△A₁B₁C₁各顶点的坐标；

⑵在y轴上找一点P ，使PA+PB₁最短，画出图形并写出P点的坐标．

查看试题解析
21. 甲、乙两商场出售相同的某种商品，每件售价均为3000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一件按原价收费，其余每件优惠20%；乙商场的优惠条件是：每件优惠25%．设所买商品为x（x＞1）件，甲商场收费为 $y_{1}$ 元，乙商场收费为y₂元．

(1)、分别求出y₁ ， y₂与x之间的关系式；

(2)、当所买商品为5件时，选择哪家商场更优惠？请说明理由．

查看试题解析
22. 如图，在Rt△ABC中，∠B＝90°，AB＝9，BC＝12，D为BC上一点，连接AD ，将△ABC沿AD折叠，使点B恰好落在边AC上的点B'处，求DB'的长度．

查看试题解析
23. 如图，直线y＝kx+4与x轴相交于点A ，与y轴相交于点B ，且AB＝2 $\sqrt{5}$ ．

(1)、求点A的坐标；

(2)、求k的值；

(3)、C为OB的中点，过点C作直线AB的垂线，垂足为D ，交x轴正半轴于点P ，试求点P的坐标及直线CP的函数表达式．

查看试题解析
24. 甲、乙两人分别从同一公路上的A ， B两地同时出发骑车前往C地，两人行驶的路程y（km）与甲行驶的时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：

(1)、A ， B两地相距 km；乙骑车的速度是 km/h；

(2)、请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式；

(3)、求甲追上乙时用了多长时间．

查看试题解析

x/kg	0	1	2	3	⋯
y/cm	14.5	15	15.5	16	⋯