吉林省长春市九台区多校联考2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，为无理数的是（）

A、 $\sqrt[3]{8}$ B、 $\sqrt{4}$ C、 $\frac{1}{3}$ D、 $\sqrt{2}$

查看试题解析
2. 若a＜ $\sqrt{7}$ ＜b ，且a与b为连续整数，则a与b的值分别为（　　）

A、1；2 B、2；3 C、3；4 D、4；5

查看试题解析
3. 下列运算正确的是（）

A、m³•m³=2m³ B、5m²n﹣4mn²=mn C、（m+1）（m﹣1）=m²﹣1 D、（m﹣n）²=m²﹣mn+n²

查看试题解析
4. 已知x，y满足 ${\begin{matrix} x + 3 y = - 1 \\ x - 3 y = 5 \end{matrix}$ ，则 $x^{2} - 9 y^{2}$ 的值为（）

A、-5 B、4 C、5 D、25

查看试题解析
5. 如图，已知AC⊥BD，垂足为O，AO＝CO，AB＝CD，则可得到△AOB≌△COD，理由是（）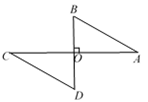

A、HL B、SAS C、ASA D、SSS

查看试题解析
6. 如图，在△ABC中，AB=AC ，以点C为圆心，以CB长为半径作圆弧，交AC的延长线于点D ，连结BD ，若∠A=32°，则∠CDB的度数（）

A、74° B、37° C、32° D、106°

查看试题解析
7. 在下列各题中，属于尺规作图的是（）

A、用直尺画一工件边缘的垂线 B、用直尺和三角板画平行线 C、利用三角板画 $45 °$ 的角 D、用圆规在已知直线上截取一条线段等于已知线段

查看试题解析
8. 如图，在△ABC中，AB=AC=BD ， ∠B=40°，则∠DAC的度数是（）

A、15° B、20° C、30° D、40°

查看试题解析

二、填空题

9. 若 $3^{x} = \frac{1}{2}$ ， $3^{y} = \frac{2}{3}$ ，则 $3^{x + y} =$ ．

查看试题解析
10. 若a+b＝3，a²+b²＝7，则ab＝．

查看试题解析
11. “两直线平行，内错角相等”的逆命题是．

查看试题解析
12. 等腰三角形的两边长分别是2和5，则这个等腰三角形的周长为．

查看试题解析
13. 如图，在△ABC中，∠A＝50°，∠B＝80°，观察图中尺规作图的痕迹，则∠DCE的度数为．

查看试题解析
14. 若 $4 x^{2} - 12 x + k$ 是完全平方式，则k的值为．

查看试题解析

三、解答题

15.

(1)、计算：
① $\sqrt{9} + \sqrt[3]{8}$ －4

② $- {(a^{4})}^{3} \cdot {(a^{2})}^{5}$

(2)、用乘法公式简算
①199×201

②97²+6×97+9

查看试题解析
16. 分解因式：

(1)、 $a^{2} - 81$

(2)、 $2 x - x^{2} - 1$

查看试题解析
17. 先化简，再求值： $(2 + x) (2 - x) + (x - 1) (x + 5)$ ，其中 $x = \frac{3}{2}$ .

查看试题解析
18. 如图，C是线段AB的中点，CD平分∠ACE ， CE平分∠BCD ， CD=CE ．

(1)、求证：AD=BE；

(2)、若∠D=56°，求∠B的度数．

查看试题解析
19. 图①、图②均是6×5的正方形网格，每个小正方形的顶点称为格点，点A、B、C均在格点上，在给定的网格中按要求画图．要求：

⑴在图①中画一个 $△$ BCD ，使△DBC≌ $△$ ABC全等；

⑵在图②中画一个 $△$ ACE使它与 $△$ ABC全等．

查看试题解析
20.
如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC．

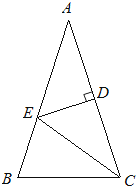(1)、求∠ECD的度数；

(2)、若CE＝5，求BC长．

查看试题解析
21. 图1在一个长为2a ，宽为2b的长方形图中，沿着虚线用剪刀均分成4块小长方形，然后按图2的形状拼成一个正方形．

(1)、图2中阴影部分的正方形边长为．

(2)、请你用两种不同的方法表示图2中阴影部分的面积，并用等式表示．

查看试题解析
22. 如图，有一座小山，现要在小山A、B的两端开一条隧道，为了知道A、B两端的距离，测量人员先过点A作直线AC⊥AB ，再在BA的延长线上找一点D ，使∠ACB=∠ACD ，这时只要量出AD的长，就知道AB的长，请你证明测量人员做法的符合题意性．

查看试题解析
23. 阅读理解并解答

(1)、我们把多项式 $a^{2} + 2 a b + b^{2}$ 和 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式，在运用完全平方公式进行因式分解时，关键是判断一个多项式是不是一个完全平方式．同样地，把一个多项式进行部分因式分解可以解决求代数式值的最大（最小）值问题
例如：（1）① $x^{2} + 6 x + 13 = (x^{2} + 6 x + 9) + 4 = {(x + 3)}^{2} + 4$

$∵ {(x + 3)}^{2} \geq 0$

$∴ {(x + 3)}^{2} + 4 \geq 4$

则代数式 $x^{2} + 6 x + 13$ 的最小值为，此时，相应的x的值为．

② $3 x^{2} - 12 x + 3 = 3 (x^{2} - 4 x) + 3$

$= 3 (x^{2} - 4 x + 4 - 4) + 3$

$= 3 (x^{2} - 4 x + 4)$ -12+3

$= 3 {(x - 2)}^{2} - 9$

$∵ {(x - 2)}^{2} \geq 0$

$∴ 3 {(x - 2)}^{2} - 9 \geq - 9$

$∴$ 代数 $3 x^{2} - 12 x + 3$ 的最小值为，此时，相应的x的值为

(2)、仿照上述方法求代数式 $- x^{2} - 8 x + 6$ 的最大（或最小）值，并求相应的x的值．

查看试题解析
24. 已知，在△ABC中，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ，垂足分别为D ， E ．

(1)、如图1，求证：△CEB≌△ADC；

(2)、如图1，求证：
①DE＝AD+BE；

②∠CAB=45°；

(3)、如图2，点O为AB的中点，连接OD ， OE ．请判断△ODE的形状？并说明理由．

查看试题解析