苏科版数学八年级上册2.5.1 等腰三角形的性质同步训练

试卷更新日期：2021-12-16 类型：同步测试

进入出卷网下载

一、单选题

1. 等腰三角形周长为13cm，其中一边长3cm，则该等腰三角形底边长为（）

A、7cm B、7cm或3cm C、3cm D、8cm

查看试题解析
2. 在△ABC中，AB＝BC ，中线AD将这个三角形的周长分成15和12两部分，则AC的长为（）

A、7 B、11 C、7或11 D、8或10

查看试题解析
3. 等腰三角形一腰上的高与另一腰的夹角为 $20 °$ ，则顶角的度数为（）

A、 $70 °$ B、 $55 °$ C、 $110 °$ D、 $70 °$ 或 $110 °$

查看试题解析
4. $△ A B C$ 中， $A B = A C$ ，点D，E分别在 $A B$ ， $A C$ 边上，且 $C D = B E$ ，则一定成立的是（）

A、 $A D = A E$ B、 $∠ A D C = ∠ A E B$ C、 $B D = C E$ D、 $∠ A B C = ∠ A C B$

查看试题解析
5. 如图所示，△ABC中，AC＝AD＝BD ， ∠DAC＝80°，则∠B的度数为（）

A、40° B、35° C、25° D、20°

查看试题解析
6. 如图，D为△ABC内一点，CD平分∠ACB ， BD⊥CD ， ∠A=∠ABD ，若AC=5，BC=3，则BD的长为（）

A、2.5 B、2 C、1.5 D、1

查看试题解析
7. 如图， $△ A B C$ 中， $∠ A = 30 ° ， A B = A C$ ，D、E分别是 $A C 、 A B$ 两点，且 $B D = B E = B C$ ，连接 $D E$ ．则 $∠ B D E$ 的度数为（）度·

A、45 B、52.5 C、67.5 D、75

查看试题解析
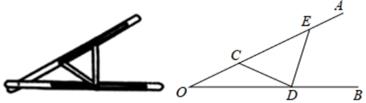
8. 如图，△ABC中，AB=AC ， AD=DE ， ∠BAD＝18°，∠EDC＝12°，则∠DAE的度数是（　　）

A、52° B、58° C、60° D、62°

查看试题解析
9. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA ， OB组成，两根棒在O点相连并可绕O转动、C点固定，OC＝CD＝DE ，点D、E可在槽中滑动．若∠BDE＝75°，
则∠CDE的度数是（）

A、60° B、65° C、75° D、80°

查看试题解析
10. 如图，在△ABC与△AEF中，AB＝AE，BC＝EF，∠ABC＝∠AEF，∠EAB＝40°，AB交EF于点D，连接EB.下列结论：①∠FAC＝40°；②AF＝AC；③∠EBC＝110°；④AD＝AC；⑤∠EFB＝40°，正确的个数为（）个.

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 等腰三角形的一个角是70°，则它的底角是．

查看试题解析
12. 用三根木棒首尾相连围成一个等腰三角形，其中两根木棒的长度分别为 $2 c m$ 和 $5 c m$ ，则第三根木棒的长为．

查看试题解析
13. 如图，在△ABC中，AB＝AC，AD是BC边上的高，点E、F是AD的三等分点，若BC＝4cm，AD＝6cm，则图中阴影部分的面积是cm².

查看试题解析
14. 如图，在△ABC中，AB=AC ， ∠A=40°，则△ABC的外角∠BCD=°．

查看试题解析
15. 如图， $∠ A B C$ ， $∠ A C B$ 的平分线相交于点 $F$ ，过点 $F$ 作 $D E / / B C$ ，交 $A B$ 于 $D$ ，交 $A C$ 于 $E$ ，那么下列结论：① $Δ B D F$ ， $Δ C E F$ 都是等腰三角形；② $D E = B D + C E$ ；③ $Δ A D E$ 的周长为 $A B + A C$ ；④ $B D = C E$ ．其中正确的是．

查看试题解析
16. 如图，在 $△ A B C$ 中，AB=AC，BC=4，面积是14，AC的垂直平分线EF分别交AC，AB边于E、F点.若点D为BC边的中点，点M为线段EF上一动点，则 $△ C D M$ 周长的最小值为.

查看试题解析
17. 四边形ABCD中，∠BAD＝125°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，当三角形AMN周长最小时，∠MAN的度数为.

查看试题解析
18. 如图，在第1个△A₁BC中，∠B=30°，A₁B=CB；在边A₁B上任取一点D，延长CA₁到A₂ ，使A₁A₂=A₁D，得到第2个△A₁A₂D；在边A₂D上任取一点E，延长A₁A₂到A₃ ，使A₂A₃=A₂E，得到第3个△A₂A₃E，…按此做法继续下去，第2021个三角形的底角度数是．

查看试题解析

三、解答题

19. 一个等腰三角形的一个内角比另一个内角的2倍少30°，求这个三角形的三个内角的度数．

查看试题解析
20. 如图，在△ABC≌△DEC，点D在AB上，且AB∥CE，∠A＝75°，求∠DCB的度数.

查看试题解析
21. 如图所示，已知点 $D$ ， $E$ 在 $△ A B C$ 的边 $B C$ 上， $A B = A C$ ， $A D = A E$ ．求证： $B D = C E$ ．

查看试题解析
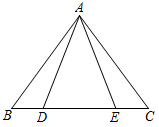22. 如图，在△ABC中，BC＝AC，∠ACB＝90°，D是AC上一点，AE⊥BD交BD的延长线于点E，且AE＝ $\frac{1}{2}$ BD.求证；BD是∠ABC的角平分线.

查看试题解析
23. 如图， $△ A B C$ 的外角平分线 $B O$ 、 $CO$ 相交于点 $O$ ， $M N$ 过点 $O$ ，且 $M N // B C$ ，分别交 $A B$ 、 $A C$ 的延长线于点 $M$ ， $N$ .求证： $M N = M B + N C$ .

查看试题解析
24. 如图所示，已知△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts.当点Q在边BC上运动时，出发多久后，△PQB能形成等腰三角形？

查看试题解析
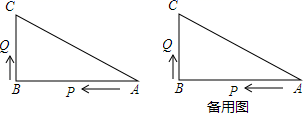25. 如图，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点（点D与A，B不重合），连结CD，将线段CD绕点C按逆时针方向旋转90°得到线段CE，连结DE交BC于点F，连接BE.

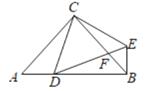(1)、求证：EB⊥AB；

(2)、当AD＝BF时，求∠BEF的度数.

查看试题解析
26. 如图，在△ABC中，点D，E分別在边AB，AC上，连结CD，BE，BD=BC=BE．

(1)、若∠A=30°，∠ACB=70°，求∠BDC，∠ACD的度数；

(2)、设∠ACD=α°，∠ABE=β°，求α与β之间的数量关系，并说明理由．

查看试题解析
27. 如图，在△ABC中，点E在BC边上，AE＝AB ，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE ，连接EF ， EF与AC交于点G ．

(1)、求证：EF＝BC ．

(2)、若∠ABC＝65°，∠ACB＝28°，求∠FGC的度数．

查看试题解析
28. 已知 $△ A B C$ 和 $△ A D E$ 均为等腰三角形，且 $∠ B A C = ∠ D A E$ ， $A B = A C$ ， $A D = A E$ ．

(1)、如图1，点 $E$ 在 $B C$ 上，求证： $B C = B D + B E$ ；

(2)、如图2，点 $E$ 在 $C B$ 的延长线上，写出 $B C$ ， $B D$ ， $B E$ 的数量关系，并说明理由，

查看试题解析

苏科版数学八年级上册2.5.1 等腰三角形的性质 同步训练

一、单选题

二、填空题

三、解答题

苏科版数学八年级上册2.5.1 等腰三角形的性质同步训练