广东省韶关市新丰县2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-12-16 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中不具有稳定性的是( )A、
2. 下列图形中不具有稳定性的是( )A、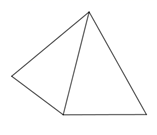 B、
B、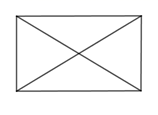 C、
C、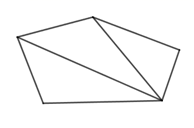 D、
D、 3. 长度分别为3,9,x的三条线段能组成一个三角形,x的值可以是( )A、4 B、5 C、6 D、74. 如图,△ABC的外角∠CAE为115°,∠C=80°,则∠B的余角为( )
3. 长度分别为3,9,x的三条线段能组成一个三角形,x的值可以是( )A、4 B、5 C、6 D、74. 如图,△ABC的外角∠CAE为115°,∠C=80°,则∠B的余角为( ) A、55° B、45° C、35° D、30°5. 已知一个多边形的每一个外角都是30°,则这个多边形的边数是( )A、12 B、11 C、10 D、96. 如图,若 ,BC=7,CF=5,则CE的长为( )
A、55° B、45° C、35° D、30°5. 已知一个多边形的每一个外角都是30°,则这个多边形的边数是( )A、12 B、11 C、10 D、96. 如图,若 ,BC=7,CF=5,则CE的长为( ) A、1 B、2 C、2.5 D、37. 下列四个图中,符合题意画出△ABC中BC边上的高是( )A、
A、1 B、2 C、2.5 D、37. 下列四个图中,符合题意画出△ABC中BC边上的高是( )A、 B、
B、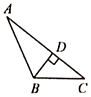 C、
C、 D、
D、 8. 如图,已知在 中,点D、E分别是边 、 的中点.若 的面积等于8,则 的面积等于( )
8. 如图,已知在 中,点D、E分别是边 、 的中点.若 的面积等于8,则 的面积等于( )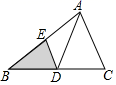 A、2 B、3 C、4 D、59. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )
A、2 B、3 C、4 D、59. 如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB , 若CD=10,则点D到AB的距离是( )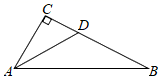 A、8 B、9 C、10 D、1110. 如图,C为线段 上一动点(不与点A、E重合),在 同侧分别作正三角形 和正三角形 , 与 交于点O, 与 交于点P, 与 交于点Q,连接 ,以下七个结论:① ;② ;③ ;④ ;⑤ ;
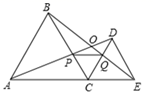
A、8 B、9 C、10 D、1110. 如图,C为线段 上一动点(不与点A、E重合),在 同侧分别作正三角形 和正三角形 , 与 交于点O, 与 交于点P, 与 交于点Q,连接 ,以下七个结论:① ;② ;③ ;④ ;⑤ ;⑥ 是等边三角形;⑦点C在 的平分线上,其中正确的有( )
 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 等腰三角形有一个内角等于110°,则它的底角等于度.12. 若点 与点 关于 轴对称,则 .13. 如图, ,D在 边上, ,则 的度数为 .
 14. 如图, , 与 交于点O , 在不添加任何辅助线的前提下要使 ,则需添加条件.
14. 如图, , 与 交于点O , 在不添加任何辅助线的前提下要使 ,则需添加条件.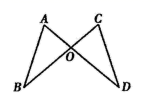 15. 如图,在 中, , , 于D点,若 ,则 .
15. 如图,在 中, , , 于D点,若 ,则 . 16. 如图,在 中,边 的垂直平分线 交 边于D点,点E为垂足.若 的周长为7cm, 的周长为11cm.则 cm.
16. 如图,在 中,边 的垂直平分线 交 边于D点,点E为垂足.若 的周长为7cm, 的周长为11cm.则 cm.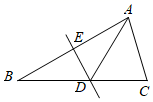 17. 如图,等边 中, 于 , ,点P、Q分别为 、 上的两个定点且 ,在 上有一动点E使 最短,则 的最小值为 .
17. 如图,等边 中, 于 , ,点P、Q分别为 、 上的两个定点且 ,在 上有一动点E使 最短,则 的最小值为 .
三、解答题
-
18. 一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.19. 如图,AF=DC , ∠BCA=∠EFD , BC=EF , 求证:△ABC≌△DEF .
 20. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
20. 如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等. (1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.21. 如图, ,直线 过点 , 直线 , 直线 ,垂足分别为 、 ,且 .
(1)、用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)、连结AD,若∠B=37°,求∠CAD的度数.21. 如图, ,直线 过点 , 直线 , 直线 ,垂足分别为 、 ,且 . (1)、求证 ;(2)、求证 .22. 如图,平面直角坐标系中A(﹣4,6),B(﹣1,2),C(﹣3,1).
(1)、求证 ;(2)、求证 .22. 如图,平面直角坐标系中A(﹣4,6),B(﹣1,2),C(﹣3,1). (1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出△A1B1C1各顶点的坐标;(2)、求△ABC的面积.23. 如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则
(1)、作出△ABC关于y轴对称的图形△A1B1C1 , 并写出△A1B1C1各顶点的坐标;(2)、求△ABC的面积.23. 如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则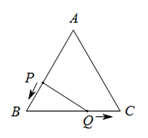 (1)、BP cm,BQ cm.(用含t的代数式表示)(2)、当t为何值时,△PBQ是直角三角形?
(1)、BP cm,BQ cm.(用含t的代数式表示)(2)、当t为何值时,△PBQ是直角三角形?

