广西百色市田东县2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，下列各点属于第四象限的是（）

A、 $(1, 2)$ B、 $(- 3, 8)$ C、 $(- 3, - 5)$ D、 $(6, - 7)$

查看试题解析
2. 下列交通标志是轴对称图形的是（）.

A、 B、 C、 D、

查看试题解析
3. 一次函数 $y = - 3 x + 2$ 的图象经过（）

A、第一、二、三象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、四象限

查看试题解析
4. 三角形的重心是三角形三条（）的交点．

A、中线 B、高 C、角平分线 D、垂直平分线

查看试题解析
5. 如图，在 $△ A B C$ 和 $△ A B D$ 中，已知 $A C = A D$ ， $B C = B D$ ，则能说明 $△ A B C ≌ △ A B D$ 的依据是（）

A、SAS B、ASA C、SSS D、HL

查看试题解析
6. 点A（﹣1，2）到x轴的距离是（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
7. 如果将一副三角板按如图方式叠放，那么 $∠ 1$ 的度数是（）

A、 $90 °$ B、 $100 °$ C、 $105 °$ D、 $135 °$

查看试题解析
8. 已知函数y＝ ${\begin{array}{l} 2 x + 1 (x \geq 0) \\ 4 x (x < 0) \end{array}$ 当x＝2时，函数值y为（）

A、5 B、6 C、7 D、8

查看试题解析
9. 下列命题中，是假命题的是（）

A、能够完全重合的两个图形全等 B、两边和一角对应相等的两个三角形全等 C、三个角都相等的三角形是等边三角形 D、等腰三角形的两底角相等

查看试题解析
10. 如图所示是函数 $y = k x + b$ 与 $y = m x + n$ 的图象，则方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解是（）

A、 $x = 4$ ， $y = 3$ B、 $x = - 4$ ， $y = - 3$ C、 $x = 3$ ， $y = 4$ D、 $x = - 3$ ， $y = - 4$

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ，AD平分 $∠ B A C$ ，DE垂直平分AC，若 $△ A D C$ 的面积等于2，则 $△ A B C$ 的面积为（）

A、2 B、3 C、4 D、6

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = A C = 8$ 厘米， $B C = 6$ 厘米，点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上，由C点向A点运动，为了使 $△ B P D ≌ △ C P Q$ ，点Q的运动速度应为（）

A、1厘米/秒 B、2厘米/秒 C、3厘米/秒 D、4厘米/秒

查看试题解析

二、填空题

13. 函数y＝ $\frac{2}{x - 3}$ 的自变量x的取值范围是.

查看试题解析
14. 已知点 $M (m + 1 ， m + 3)$ 在x轴上，则m等于.

查看试题解析
15. 小芳有两根长度为5cm和10cm的木条，她想钉一个三角形木框，她应该再选择一根长度为cm的木条.（只需写出其中一种）

查看试题解析
16. 已知一次函数 $y = - x + 6$ 的图象上有两点 $A (- 1, y_{1})$ ， $A (2, y_{2})$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是.

查看试题解析
17. 如图所示的是一张直角 $△ A B C$ 纸片（ $∠ C = 90 °$ ），其中 $∠ B A C = 30 °$ ，如果用两张完全相同的这种纸片恰好能拼成如图2所示的 $△ A B D$ ，若 $B C = 2$ ，则 $△ A B D$ 的周长为.

查看试题解析
18. 正方形 $A_{1} B_{1} C_{1} O$ 、 $A_{2} B_{2} C_{2} C_{1}$ 、 $A_{3} B_{3} C_{3} C_{2}$ ……按如图的方式放置，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ …和点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ …分别在直线 $y = k x + b (k > 0)$ 和x轴上，已知点 $B_{1} (1 ， 1)$ ， $B_{2} (3 ， 2)$ ，按此规律，则点 $B_{4}$ 的坐标是.

查看试题解析

三、解答题

19. 已知在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为： $A (- 3 ， - 1)$ ， $B (- 2 ， - 4)$ ， $C (1 ， - 3)$ .

⑴作出 $△ A B C$ ；

⑵若将 $△ A B C$ 向上平移3个单位后再向右平移2个单位得到 $△ A_{1} B_{1} C_{1}$ ，请作出 $△ A_{1} B_{1} C_{1}$ .

查看试题解析
20. 已知：一次函数 $y = k x + b$ 的图象经过 $M (0 ， 2)$ ， $N (1 ， 3)$ 两点.

(1)、求一次函数的解析式，并画出此一次函数的图象；

(2)、求当x取何值时，函数值 $y > 0$ .

查看试题解析
21. 如图，已知 $A B = A C$ ， $D B = D C$ ，E是AD上的一点，求证： $B E = C E$ .

查看试题解析
22. 尺规作图：某学校正在进行校园环境的改造工程设计，准备在校内一块四边形花坛内栽上一棵桂花树.如图，要求桂花树的位置点P，到花坛的两边AB，BC的距离相等，并且点P到点A，D的距离也相等.请用尺规作图作出栽种桂花树的位置点P（不写作法，保留作图痕迹）.

查看试题解析
23. 如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD，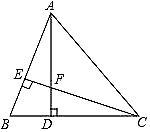

(1)、求证：△ABD≌△CFD；

(2)、已知BC=7，AD=5，求AF的长。

查看试题解析
24. 已知 $△ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ，点D为BC边上一点，连接AD，作 $D E ⊥ A B$ 于点E， $D F ⊥ A C$ 于点F.

(1)、若AD为 $△ A B C$ 的角平分线（如图1），图中 $∠ 1$ 、 $∠ 2$ 有何数量关系？请说明理由.

(2)、若AD为 $△ A B C$ 的高（如图2），求图中 $∠ 1$ 、 $∠ 2$ 的度数.

查看试题解析
25. 某县举办运动会需购买A，B两种奖品，若购买A种奖品5件和B种奖品2件，共需80元；若购买A种奖品3件和B种奖品3件，共需75元.

(1)、求A、B两种奖品的单价各是多少元？

(2)、大会组委会计划购买A.B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式，并求出自变量m的取值范围，以及确定最少费用W的值.

查看试题解析
26. 已知正比例函数 $y = \frac{4}{3} x$ 与一次函数 $y = 3 x - 5$ 的图象交于点A，且 $O A = O B$ .

(1)、求A点坐标；

(2)、求 $△ A O B$ 的面积；

(3)、已知在x轴上存在一点P，能使 $△ A O P$ 是等腰三角形，请直接写出所有符合要求的点P的坐标.

查看试题解析