广东省江门市恩平市2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. 正五边形的外角和是（）

A、 $180 °$ B、 $360 °$ C、 $540 °$ D、 $720 °$

查看试题解析
2. 下列长度的三条线段不能组成三角形的是（）

A、3，4，5 B、6，10，8 C、2，3，6 D、2，2，3

查看试题解析
3. 等腰三角形的一个底角等于 $55 °$ ，则它的顶角等于（）

A、 $45 °$ B、 $55 °$ C、 $70 °$ D、 $80 °$

查看试题解析
4. 下面四个图形分别是绿色食品、节水、节能和回收标志，在这四个标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 下列图形是全等图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如图， $A C$ 与 $B D$ 相交于点O，且 $A O = C O$ ， $B O = D O$ ，则图中全等三角形共有（）

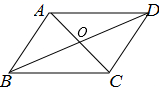A、2对 B、4对 C、5对 D、6对

查看试题解析
7. 如图，已知 $△ A B C ≅ △ C D E$ ，下列结论中错误的是（）

A、 $A C = C E$ B、 $∠ B A C = ∠ E C D$ C、 $∠ B = ∠ D$ D、 $∠ A C B = ∠ E C D$

查看试题解析
8. 三角形的下列线段中能将三角形的面积分成相等两部分的是（）

A、中线 B、角平分线 C、高 D、线段的垂直平分线

查看试题解析
9. 如图，在△ABC中，∠B＝70°，∠C＝25°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于M ， N ，作直线MN ，交BC于D ，连接AD ，则∠BAD的度数是（）

A、50° B、60° C、65° D、75°

查看试题解析
10. 如图，把长方形ABCD沿EF对折后使两部分重合，若∠AEF=110°，则∠1=（　　）

A、50° B、35° C、30° D、40°

查看试题解析

二、填空题

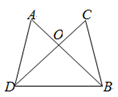
11. 在三角形 $A B C$ 中，已知 $∠ A = 70 °$ ， $∠ B = 40 °$ ，那么 $△ A B C$ 的形状是．

查看试题解析
12. 在△ABC中，AB=AC=5cm ， ∠B=60°，则BC= cm．

查看试题解析
13. 若点 $P (3 ， - 4)$ ，则点P关于y轴对称的点为．

查看试题解析
14. 如图，AB，CD相交于点O，AD＝CB，请你补充一个条件，使得△AOD ≌△COB．你补充的条件是．

查看试题解析
15. 如图，在△ABC中，AD⊥BC于点D ， BD＝DC ，若BC＝6，AD＝7，则图中阴影部分图形的面积为．

查看试题解析
16. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ C = 30^{\circ}$ ， $A D ⊥ A B$ ，交 $B C$ 于点D，且 $A D = 1$ ，则 $B C =$ ．

查看试题解析
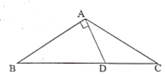17. 如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于．

查看试题解析
18. 如图，△ABC≌△DCB ，若AC＝7，BE＝5，则DE的长为．

查看试题解析

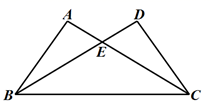
三、解答题

19. 如图， $∠ A C D = 140 °$ ， $∠ A = 60 °$ ，求 $∠ B$ ， $∠ A C B$ 的度数．

查看试题解析
20. 如图所示，在 $Δ A B C$ 中， $A D$ 是 $∠ B A C$ 平分线， $A D$ 的垂直平分线分别交 $A B ， B C$ 延长线于点 $F ， E$ .求证： $D F / / A C$ .

证明：∵ $A D$ 平分 $∠ B A C$

∴ $∠$ ▲    $= ∠$   ▲ (角平分线的定义)

∵ $E F$ 垂直平分 $A D$

∴ ▲ $=$   ▲ （线段垂直平分线上的点到线段两个端点距离相等）

∴ $∠ B A D = ∠ A D F$ （                 ）

∴ $∠ D A C = ∠ A D F$ （等量代换）

∴ $D F / / A C$ （                 ）

查看试题解析
21. 如图，在8×8的网格中的每个小正方形边长都是1，线段交点称作格点．任意连接这些格点，可得到一些线段．按要求作图：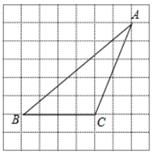

(1)、①请画出△ABC的高AD；
②请连接格点，用一条线段将图中△ABC分成面积相等的两部分；

(2)、直接写出△ABC的面积是.

查看试题解析
22. 已知：如图，∠B＝∠C＝90°， AF=DE ， BE=CF ．求证：AB=DC ．

查看试题解析
23. 将一副直角三角板按如图放置（其中 $∠ C = ∠ E = 90 °$ ），使含 $30 °$ 角的三角板 $D E F$ 的较长直角边 $E F$ 与等腰直角三角板 $A B C$ 的斜边 $A B$ 平行，求 $∠ 1$ 的度数．

查看试题解析
24. 阅读下列材料，并完成相应任务．
小学时候我们就知道三角形内角和是180度，学习了平行线之后，可以证明三角形内角和是180度，证明方法如下：

如图1，已知：三角形 $A B C$ ，求证 $∠ A B C + ∠ A C B + ∠ B A C = 180 °$ ．

证法一：如图2，过点A作直线DE∥BC ，

∵ $D E / / B C$ ，∴ $∠ A B C = ∠ D A B$ ， $∠ A C B = ∠ C A E$ ，

∵ $∠ D A B + ∠ B A C + ∠ C A E = 180 °$ ，∴ $∠ A B C + ∠ A C B + ∠ B A C = 180 °$ ，

即三角形内角和是 $180 °$ ．

证法二：如图3，延长 $B C$ 至M，过点C作CN∥AB ，

…

(1)、任务：（1）证法一的思路是用平行线的性质得到 $∠ A B C = ∠ D A B$ ， $∠ A C B = ∠ C A E$ ，将三角形内角和问题转化为一个平角，进而得到三角形内角和是 $180 °$ ，这种方法主要体现的数学思想是（将正确选项代码填入空格处）

A ．数形结合思想，B ．分类思想，C ．转化思想，D ．方程思想

(2)、将证法二补充完整．

查看试题解析
25. 等腰 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，点A、点B分别是x轴、y轴两个动点，直角边 $A C$ 交x轴于点D，斜边 $B C$ 交y轴于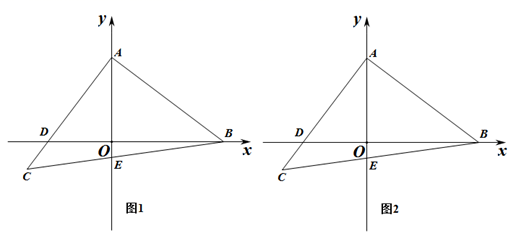点E．

(1)、如图（1），若 $A (0 ， 1)$ ， $B (2 ， 0)$ ，求C 点的坐标；

(2)、如图（2），在等腰 $R t △ A B C$ 不断运动的过程中，若满足 $B D$ 始终是 $∠ A B C$ 的平分线，试探究：线段 $O A$ 、 $O D$ 、 $B D$ 三者之间是否存在某一固定的数量关系，并说明理由．

查看试题解析