甘肃省兰州市教学管理第五片区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-12-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，属于无理数的是（）

A、3.14 B、 $\frac{22}{7}$ C、 $\sqrt{4}$ D、 $π$

查看试题解析
2. △ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（　　）

A、∠A+∠B=∠C B、∠A：∠B：∠C=1：2：3 C、a²=c²﹣b² D、a：b：c=3：4：6

查看试题解析
3. 下列图形中，由 $∠ 1 = ∠ 2$ 能得到 $A B / / C D$ 的是（）

A、 B、 C、 D、

查看试题解析
4. 下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列各式中正确的是（）

A、 $\sqrt{16}$ =±4 B、 $\sqrt{{(- 2)}^{2}}$ =2 C、 $\sqrt{27}$ =3 D、 $\frac{1}{\sqrt{3}}$ = $\sqrt{3}$

查看试题解析
6. 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（）

A、﹣5 B、﹣3 C、3 D、1

查看试题解析
7. 若方程组 ${\begin{array}{l} 2 x + y = 1 - 3 k \\ x + 2 y = 2 \end{array}$ 的解满足 $x + y = 0$ ，则 $k$ 的值为（）

A、-1 B、1 C、0 D、不能确定

查看试题解析
8. 已知点 $(- 4 ， y_{1}) ， (2 ， y_{2})$ 都在直线 $y = \frac{1}{2} x + 2$ 上，则 $y_{1}$ 和 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法确定

查看试题解析
9. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 和 $y = m x + n$ 相交于点 $(2 ， - 1)$ ，则关于 $x ， y$ 的方程组 ${\begin{matrix} y = k x + b \\ y = m x + n \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$

查看试题解析

10. 九年级（1）班甲、乙、丙、丁四名同学几次数学测试成绩的平均数

\bar{x}

（分）及方差S²如下表：

	甲	乙	丙	丁
平均数（分）	95	97	95	97
方差	0.5	0.5	0.2	0.2

老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛，那么应选（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

11. 我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有 $x$ 匹，小马有 $y$ 匹，则可列方程组为（）

A、 ${\begin{matrix} x + y = 100 \\ \frac{1}{3} x + 3 y = 100 \end{matrix}$ B、 ${\begin{matrix} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{matrix}$ C、 ${\begin{matrix} x + y = 100 \\ x + 3 y = 100 \end{matrix}$ D、 ${\begin{matrix} x + y = 100 \\ 3 x + y = 100 \end{matrix}$

查看试题解析
12. 如图，点A，B，C在一次函数y= -2x+m的图象上，它们的横坐标依次为-1，1，2，分别过这些点作x轴与y轴的垂线，则图中的阴影部分的面积之和是（）

A、1 B、3 C、3（m-1） D、 $\frac{3}{2} (m - 2)$

查看试题解析

二、填空题

13. 将直线y＝2x＋1向下平移3个单位长度后所得直线的表达式是．

查看试题解析
14. 已知 $2 x^{n - 3} - \frac{1}{3} y^{2 m + 1} = 0$ 是关于x,y的二元一次方程，则 $n^{m} =$ .

查看试题解析
15. 如图，∠AOB=40°，OP平分∠AOB，点C为射线OP上一点，作CD⊥OA于点D，在∠POB的内部作CE∥OB，则∠DCE=度.

查看试题解析
16. 如图，正方形纸片 $A B C D$ 的边长为3，点 $E$ 、 $F$ 分别在边 $B C$ 、 $C D$ 上，将 $A B$ 、 $A D$ 分别沿 $A E$ 、 $A F$ 折叠，点 $B$ 、 $D$ 恰好都落在点 $G$ 处，已知 $B E = 1$ ，则 $E F$ 的长为.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(1 - π)}^{0} + | \sqrt{2} - \sqrt{3} | - \sqrt{12} + {(\frac{1}{\sqrt{2}})}^{- 1}$

(2)、 $\frac{\sqrt{50} \times \sqrt{32}}{\sqrt{8}} - 4$

查看试题解析
18. 解方程组 ${\begin{array}{l} 3 x = 5 y \\ 5 x - y = 1 \end{array}$

查看试题解析
19. 解方程组： ${\begin{cases} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3 x + 2 y = 10 \end{cases}$

查看试题解析
20. 已知2a-1的平方根是±3，3a+b-1的算术平方根是4，求a+2b的值．

查看试题解析
21. 如图，正方形网格中的 $△ A B C$ ，若小方格边长为1，请证明 $△ A B C$ 为直角三角形，并求出其面积.

查看试题解析
22. 如图，EF∥BC，AC平分∠BAF，∠B=80°.求∠C的度数.

查看试题解析
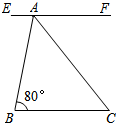23. 如图，过点A的一次函数的图象与正比例函数y＝2x的图象相交于点B．

(1)、求该一次函数的解析式；

(2)、若该一次函数的图象与x轴交于点D，求△BOD的面积．

查看试题解析
24. 如图，已知∠1+∠2＝180°，∠3＝B，

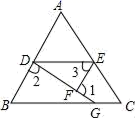(1)、证明：EF∥AB.

(2)、试判断∠AED与∠C的大小关系，并说明你的理由.

查看试题解析
25. 为了解某校八年级学生一门课程的学习情况，小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.小佳对八年级1班全班学生（25名）的成绩进行分析，过程如下收集、整理数据:
表一：

分数段

班级

$60 \leq x < 70$

$70 \leq x < 80$

$80 \leq x < 90$

$90 \leq x < 100$

八年级1班

7

5

10

3

表二：

统计量

班级

平均数

中位数

众数

极差

方差

八年级1班

78

85

36

105.28

小丽用同样的方式对八年级2班全班学生（25名）的成绩进行分析，变数据如下：

统计量

班级

平均数

中位数

众数

极差

方差

八年级2班

75

76

73

44

146.8

根据以上信息，解决下列问题:

(1)、已知八年级1班学生的成绩处在 $80 \leq x < 90$ 这一组的数据如下: $85, 87, 88, 80, 82, 85, 83, 85, 87, 85$ .根据上述数据，将表二补充完整:

(2)、你认为哪个班级的成绩更为优异？请说明理由

查看试题解析
26. 已知甲、乙两地相距90km，A，B两人沿同一公路从甲地出发到乙地，A骑摩托车，B骑电动车，图中DE，OC分别表示A，B离开甲地的路程 $s (km)$ 与时间 $t (h)$ 的函数关系的图象，根据图象解答下列问题．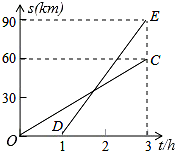

(1)、A比B后出发几个小时？B的速度是多少？

(2)、在B出发后几小时，两人相遇？

查看试题解析
27. 亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位.

(1)、计划调配36座新能源客车多少辆？该大学共有多少名志愿者？

(2)、若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？

查看试题解析
28. 如图，直线l的解析式为y=﹣ $\frac{4}{3}$ x+b，它与坐标轴分别交于A、B两点，其中点B坐标为（0，4）.

(1)、求出A点的坐标；

(2)、在第一象限的角平分线上是否存在点Q使得∠QBA=90°？若存在，求点Q的坐标；若不存在，请说明理由.

(3)、动点C从y轴上的点（0，10）出发，以每秒1cm的速度向负半轴运动，求出点C运动所有的时间t，使得△ABC为轴对称图形（直接写答案即可）

查看试题解析