苏科版数学八年级上册 2.4.3 线段、角的轴对称性 同步训练
试卷更新日期:2021-12-16 类型:同步测试
一、单选题
-
1. 在联合会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三边上高的交点2. 如图,在 ABC中,DE是AB的垂直平分线,BC上的点F在AC的垂直平分线上,若AB=6,AC=8,BC=12,则 AEF的周长是( )
 A、6 B、8 C、10 D、123. 如图,AD是△ABC的角平分线,DF⊥AB于点F , 且DE=DG , S△ADG=24,S△AED=18,则△DEF的面积为( )
A、6 B、8 C、10 D、123. 如图,AD是△ABC的角平分线,DF⊥AB于点F , 且DE=DG , S△ADG=24,S△AED=18,则△DEF的面积为( ) A、2 B、3 C、4 D、64. 如图, 平分 交 于点D, 于点E, 于点F.若 , , ,则 的长是( )
A、2 B、3 C、4 D、64. 如图, 平分 交 于点D, 于点E, 于点F.若 , , ,则 的长是( ) A、8 B、7 C、6 D、55. 如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( )
A、8 B、7 C、6 D、55. 如图,AB∥CD,BE和CE分别平分∠ABC和∠BCD,AD过点E,且与AB互相垂直,点P为线段BC上一动点,连接PE.若AD=8,BC=10,则PE的最小值为( ) A、8 B、5 C、4 D、26. 在 中,已知 ,AD是 的角平分线, 于点E.若 的面积为S,则 的面积为( )A、 B、 C、 D、7. 如图, 中, 的平分线 与边 的垂直平分线 相交于点D, 交 的延长线于点E, 于F,现有下列结论:① ;② ;③ 平分 ;④ ;其中,正确的结论的个数是______
A、8 B、5 C、4 D、26. 在 中,已知 ,AD是 的角平分线, 于点E.若 的面积为S,则 的面积为( )A、 B、 C、 D、7. 如图, 中, 的平分线 与边 的垂直平分线 相交于点D, 交 的延长线于点E, 于F,现有下列结论:① ;② ;③ 平分 ;④ ;其中,正确的结论的个数是______ A、4 B、3 C、2 D、18. 如图,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于G,DE⊥AB于E,则下列结论①∠A=∠BCF,②CD=CG,③AD=BD,④BC=BE中正确的个数是( )
A、4 B、3 C、2 D、18. 如图,Rt△ABC中,CF是斜边AB上的高,角平分线BD交CF于G,DE⊥AB于E,则下列结论①∠A=∠BCF,②CD=CG,③AD=BD,④BC=BE中正确的个数是( )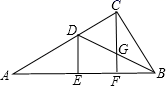 A、1 B、2 C、3 D、49. 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论:
A、1 B、2 C、3 D、49. 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论:①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE,④DE=DF.其中正确的是( )
 A、①②③ B、①②④ C、①② D、①③10. 如图,△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,下面四个结论:①∠AEF=∠AFE;②AD垂直平分EF ;③ ;④E一定平行于BC.其中正确的是( )
A、①②③ B、①②④ C、①② D、①③10. 如图,△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,下面四个结论:①∠AEF=∠AFE;②AD垂直平分EF ;③ ;④E一定平行于BC.其中正确的是( ) A、①②③ B、②③④ C、①③④ D、①②③④
A、①②③ B、②③④ C、①③④ D、①②③④二、填空题
-
11. 如图,在 中, 分别以 为圆心, 为半径画弧交于两点,过这两点的直线交AC于点,连接BD,则△BCD的周长是 .
 12. 通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为 .
12. 通过学习我们已经知道三角形的三条内角平分线是交于一点的.如图,P是△ABC的内角平分线的交点,已知P点到AB边的距离为1,△ABC的周长为10,则△ABC的面积为 . 13. 如图, 中, ,DE垂直平分AB, , ,则 .
13. 如图, 中, ,DE垂直平分AB, , ,则 . 14. 如图,△ABC中,∠CAB和∠CBA的角平分线交于点P,连接PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3 , 则S1S2+S3.(填“>“<”或“=”)
14. 如图,△ABC中,∠CAB和∠CBA的角平分线交于点P,连接PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3 , 则S1S2+S3.(填“>“<”或“=”) 15. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是.
15. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是. 16. 如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=.
16. 如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=. 17. 如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为.
17. 如图,在△ABC中,∠BAC=80°,DE,FG分别是AB,AC边的垂直平分线,点E、F在BC上,则∠FAE的度数为. 18. 如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为.
18. 如图,钝角三角形ABC的面积为15,最长边AB=10,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值为.
三、解答题
-
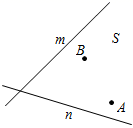
19. 为了加强环境治理,某地准备在如图所示的公路m、n之间的S区域新建一座垃圾处理站P,按照设计要求,垃圾处理站P到区域S内的两个城镇A、B的距离必须相等,到两条公路m、n的距离也必须相等.请在图中用尺规作图的方法作出点P的位置并标出点P(不写作法但保留作图痕迹).
 20. 如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。
20. 如图,在△ABC 中,∠BAC =80°,AB、AC 的垂直平分线分别与BC 交于 D、E,求∠EAD 的度数。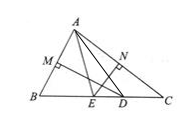 21. 已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
21. 已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长. 22. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
22. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.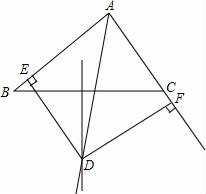 23. 已知:在 中,AD平分 , 于F, 于 线段AD与EF有何关系?并说明理由.
23. 已知:在 中,AD平分 , 于F, 于 线段AD与EF有何关系?并说明理由. 24. 如图,在△ABC中,AD为∠BAC的平分线,FE垂直平分AD,交AD于E,交BC的延长线于F,那么∠B与∠CAF相等吗?为什么?
24. 如图,在△ABC中,AD为∠BAC的平分线,FE垂直平分AD,交AD于E,交BC的延长线于F,那么∠B与∠CAF相等吗?为什么? 25. 如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
25. 如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF. (1)、求证:AD=CE.(2)、若CD=5,AC=6,求△AEB的面积.26. 如图,DE⊥AB于E , DF⊥AC于F , 若BD =CD、BE=CF .
(1)、求证:AD=CE.(2)、若CD=5,AC=6,求△AEB的面积.26. 如图,DE⊥AB于E , DF⊥AC于F , 若BD =CD、BE=CF . (1)、求证:AD平分∠BAC;(2)、已知AB=5,AC=8,求BE的长.
(1)、求证:AD平分∠BAC;(2)、已知AB=5,AC=8,求BE的长.

