安徽省淮南市寿县2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-12-16 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,点 在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列四个图形中,线段BD是△ABC的高的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在椭圆形池塘的一侧选取一点O , 测得OA=5米,OB=11米,则A点到B点的距离可能是( )
3. 如图,在椭圆形池塘的一侧选取一点O , 测得OA=5米,OB=11米,则A点到B点的距离可能是( ) A、5米 B、10米 C、16米 D、17米4. 函数y= 中的自变量x的取值范围是( )A、x>0 B、x≥﹣1 C、x>0且x≠﹣1 D、x≥﹣1且x≠05. 在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A的坐标为 (-2 , 2 ) ,则点 B’的坐标为( )A、( 3 , 4 ) B、( 4 , 3 ) C、(一l ,一2 ) D、(-2,-1)6. 关于函数y=2x﹣1,下列结论成立的是( )A、当x<0时,y<0 B、当x>0时,y>0 C、图象必经过点(0,1) D、图象不经过第三象限7. 已知两个一次函数y=kx+5和y=2x+1的图象交于A(m , 3),则一次函数y=kx+5的图象所在的象限为( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限8. 如图,△ABC的三条高AD , BE , CF相交于点H , 下列结论错误的是( )
A、5米 B、10米 C、16米 D、17米4. 函数y= 中的自变量x的取值范围是( )A、x>0 B、x≥﹣1 C、x>0且x≠﹣1 D、x≥﹣1且x≠05. 在平面直角坐标系中,已知线段AB的两个端点分别是A(- 4 ,-1).B(1,1) 将线段AB平移后得到线段A ’B’,若点A的坐标为 (-2 , 2 ) ,则点 B’的坐标为( )A、( 3 , 4 ) B、( 4 , 3 ) C、(一l ,一2 ) D、(-2,-1)6. 关于函数y=2x﹣1,下列结论成立的是( )A、当x<0时,y<0 B、当x>0时,y>0 C、图象必经过点(0,1) D、图象不经过第三象限7. 已知两个一次函数y=kx+5和y=2x+1的图象交于A(m , 3),则一次函数y=kx+5的图象所在的象限为( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限8. 如图,△ABC的三条高AD , BE , CF相交于点H , 下列结论错误的是( ) A、∠DAC=∠CBE B、∠ACF=∠ABE C、∠ABC=∠CHD D、∠BHD=∠BAC9. 已知A , B两地相距60km,甲从A地去B地,乙从B地去A地,图中l1 , l2分别表示甲、乙两人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.设两人相遇在P处,则PA的距离为( )
A、∠DAC=∠CBE B、∠ACF=∠ABE C、∠ABC=∠CHD D、∠BHD=∠BAC9. 已知A , B两地相距60km,甲从A地去B地,乙从B地去A地,图中l1 , l2分别表示甲、乙两人离B地的距离y(km)与甲出发时间x(h)的函数关系图象.设两人相遇在P处,则PA的距离为( ) A、42km B、28km C、24km D、18km10. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )
A、42km B、28km C、24km D、18km10. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )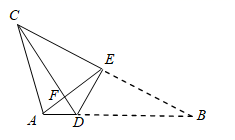 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点P(-2,3)到y轴距离为 .12. 命题“如果ab=0,那么a+b=0”的逆命题为 .13. 如图所示是某零件的平面图,其中∠B=∠C=30°,∠A=40°,则∠ADC 的度数为 .
 14. 在平面直角坐标系xOy中,已知直线l:y=kx+b , 其中k , b为常数,且k≠0.请完成下列问题:(1)、若直线l与直线y=﹣2x平行,且l与x轴交于点A(2,0),与y轴交于点B , 则△AOB的面积为 .(2)、若k=b+3,则不论k取何值,直线l一定经过某一个点,则该点的坐标为 .
14. 在平面直角坐标系xOy中,已知直线l:y=kx+b , 其中k , b为常数,且k≠0.请完成下列问题:(1)、若直线l与直线y=﹣2x平行,且l与x轴交于点A(2,0),与y轴交于点B , 则△AOB的面积为 .(2)、若k=b+3,则不论k取何值,直线l一定经过某一个点,则该点的坐标为 .三、解答题
-
15. 已知y与x+3成正比例,且当x=0时,y=﹣6.当x=1时,求y的值.16. 若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣2|c﹣a﹣b|+3|a+b+c|的值.
17. 如图,已知直线y=ax+b与直线y=cx+d相交于点P( , ).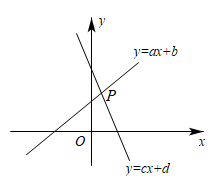 (1)、求2a+3b的值;(2)、观察图象,直接写出ax+b<cx+d的解集.18. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)、求2a+3b的值;(2)、观察图象,直接写出ax+b<cx+d的解集.18. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.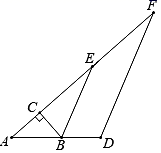 (1)、求∠CBE的度数;(2)、若∠F=25°,求证:BE∥DF.19. 如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(﹣4,1),B(﹣3,﹣4).
(1)、求∠CBE的度数;(2)、若∠F=25°,求证:BE∥DF.19. 如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(﹣4,1),B(﹣3,﹣4). (1)、将线段AB向上平移2个单位,再向右平移5个单位得到线段A′B′,画出线段A′B′(点A′,B′分别为A , B的对应点);(2)、若点P(m , n)为线段AB上任意一点,经过(1)的平移后,在线段A′B′上对应的点P′的坐标为 ;(3)、△B′AB的面积为 .20. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE AB , EF BC , 且DE交BC于点P , ∠ABC与∠DEF有怎样的数量关系?
(1)、将线段AB向上平移2个单位,再向右平移5个单位得到线段A′B′,画出线段A′B′(点A′,B′分别为A , B的对应点);(2)、若点P(m , n)为线段AB上任意一点,经过(1)的平移后,在线段A′B′上对应的点P′的坐标为 ;(3)、△B′AB的面积为 .20. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE AB , EF BC , 且DE交BC于点P , ∠ABC与∠DEF有怎样的数量关系? (1)、我们发现∠ABC与∠DEF有两种位置关系,如图1与图2所示.
(1)、我们发现∠ABC与∠DEF有两种位置关系,如图1与图2所示.①图1中∠ABC与∠DEF数量关系为 ;图2中∠ABC与∠DEF数量关系为 ;
②由①得出一个真命题(用文字叙述) .
(2)、应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请求出这两个角的度数.
21. 为更新果树品种,某果园计划新购进A , B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)(x≤0≤45,x为整数)之间存在如图所示的函数关系. (1)、求y与x的函数关系式;(2)、若在购买计划中,B种苗的数量不少于22棵但不超过35棵,请设计购买方案,使总费用最低,并求出最低费用.22. 如图,在△ABC中,D , E分别是BC和AB上的点,AD、CE相交于F .
(1)、求y与x的函数关系式;(2)、若在购买计划中,B种苗的数量不少于22棵但不超过35棵,请设计购买方案,使总费用最低,并求出最低费用.22. 如图,在△ABC中,D , E分别是BC和AB上的点,AD、CE相交于F . (1)、若AD , CE分别平分∠BAC和∠ACB , 已知∠B=40°,求∠AFE的度数;(2)、设BC=a , AC=b , AB=c , 若△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,求AE和BD的长.(用含a、b、c的式子表示)23. 在平面直角坐标系中,已知直线AB:y=kx+b(k , b为常数,且k≠0)分别与x轴、y轴的正半轴相交于A , B两点.(1)、若A , B两点的坐标分别为A(2,0),B(0,4)时,求k , b的值;(2)、若直线CD平行于(1)中的直线AB , 且分别与x , y的正半轴相交于点C , D , 已知四边形ACDB的面积为12,求直线CD的函数表达式;(3)、已知P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,求直线AB的函数表达式.
(1)、若AD , CE分别平分∠BAC和∠ACB , 已知∠B=40°,求∠AFE的度数;(2)、设BC=a , AC=b , AB=c , 若△ABD与△ACD的周长相等,△CAE与△CBE的周长相等,求AE和BD的长.(用含a、b、c的式子表示)23. 在平面直角坐标系中,已知直线AB:y=kx+b(k , b为常数,且k≠0)分别与x轴、y轴的正半轴相交于A , B两点.(1)、若A , B两点的坐标分别为A(2,0),B(0,4)时,求k , b的值;(2)、若直线CD平行于(1)中的直线AB , 且分别与x , y的正半轴相交于点C , D , 已知四边形ACDB的面积为12,求直线CD的函数表达式;(3)、已知P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,求直线AB的函数表达式.