苏科版数学八年级上册2.4.2 角的轴对称性 同步训练
试卷更新日期：2021-12-16 类型：同步测试
一、单选题
-
1. △ABC的两条角平分线AD ， BE相交于点F ， 下列结论一定正确的是（ ）
A、BD = DC B、BE⊥AC C、FA = FB D、点F到三角形三边的距离都相等2. 如图，在 中， 平分 交 于点D ， ，若点P是 上的动点，则线段 的最小值是（ ）
A、2.4 B、3 C、4 D、53. 如图，BD是∠ABC的角平分线，DE⊥AB于E，△ABC的面积是30cm2 ， AB=14cm，BC=16cm，则DE的长度为（ ）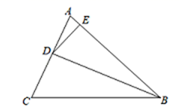
A、1cm B、2cm C、3cm D、4cm4. 如图，△ABC的三边AB，BC，CA的长分别为8，12，10，其三条角平分线将△ABC分为三个三角形，则S△ABO：S△BCO：S△AOC等于（ ）
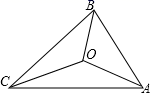A、1：1：1 B、2：4：3 C、4：6：5 D、4：6：105. 如图，已知 ABC的周长是34，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD＝4，则 ABC的面积是（ ）
A、17 B、34 C、38 D、686. 如图， ABC中，∠C＝90°，AD平分∠BAC，AB＝5，AC＝3，则BD的长是（ ）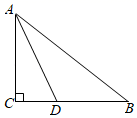
A、2 B、3.5 C、3 D、2.57. 如图，BP平分∠ABC，D为BP上一点，点E，F分别在BA，BC上，且满足DE=DF．若∠BED=140°，则∠BFD的度数是（ ）
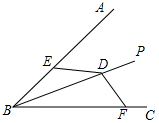A、40° B、50° C、60° D、70°8.如图所示，P，Q分别是BC，AC上的点，作PR⊥AB于R点，作PS⊥AC于S点，若AQ=PQ，PR=PS，下面三个结论：①AS=AR；②QP∥AR；③△BRP≌△CSP，正确的是（ ）
A、①和③ B、②和③ C、①和② D、①，②和③9. 如图，△ABC中，∠ACF、∠EAC的角平分线BP、AP交于点P ， 延长BA、BC ， PM⊥BE ， PN⊥BF ． 则下列结论中：①BP平分∠ABC；②∠ABC+2∠APC＝180°；③∠CAB＝2∠CPB；④S△PAC＝S△MAP+S△NCP ． 正确的个数（ ）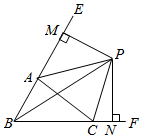
A、1个 B、2个 C、3个 D、4个10. 如图， 的外角 ， 的平分线 ， 相交于点P， 于E， 于F，下列结论：（1） ；（2）点P在 的平分线上；（3） ；（4）若 ，则 ，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是28 ，AB＝20cm，AC＝8cm，则DE=cm．
12. 如图，已知 的面积是20， ， 分别平分 和 ， 于D ， 且 ，则 的周长是 ．
13. 有三条两两相交的公路，要建一个加油站，使它到三条公路的距离相等，那么加油站可建的地点有个.
14. 如图，在 中， 是 的平分线， 于点E ， 已知 ，则 的值为 ．
15. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是.
16. 如图，已知BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=.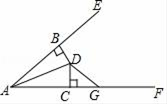
17. 如图，点P是∠AOB的角平分线OC上一点，PN⊥OB于点N，点M是线段ON上一点．已知OM＝3，ON＝5，点D为OA上一点，若满足PD＝PM，则OD的长度为 ．
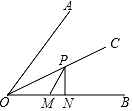18. 如图， 于 ， 于 ，若 ，则下列结论：① ；② 平分 ；③ ；④ 中 正确的是.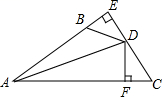
三、解答题
-
19. 请在△ABC内部找到一个点P，使点P到AB、BC的距离相等，且PB=PC。(尺规作图，保留作图痕迹，不写作法)．
20. 如图，已知OE平分∠AOB，BC⊥OA于点C，AD⊥OB于点D，求证：EA=EB．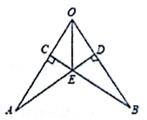
21. 如图，点D、B分别在∠A的两边上，C是∠A内一点，AB = AD，BC = CD，CE⊥AD于E，CF⊥AF于F.求证：CE = CF.
22. 如图， ，M是BC的中点，DM平分 ，求证：AM平分 ．
23. 在锐角三角形ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于F，且BE=CF，求证：AD是∠BAC的平分线；
24. 如图，在△ABC中，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F．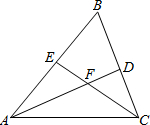
(1)、求证：∠EFA=90°- ∠B；(2)、若∠B=60°，求证：EF=DF．25. 如图，在 中，点D是BC边上一点，连接AD ．
(1)、若点D是BC的中点，则 ；(2)、若AD是 的角平分线，求证 ；(3)、若点D是BC的中点，且AD是 的角平分线，请判断 的形状及AD与BC的位置关系，并说明理由，26. 如图，DE⊥AB于E ， DF⊥AC于F ， 若BD ＝CD、BE＝CF ．
(1)、求证：AD平分∠BAC；(2)、已知AB＝5，AC＝8，求BE的长．27. 如图，在△ABC中，AC＝6cm ， AB＝9cm ， D是边BC上一点，AD平分∠BAC ， 在AB上截取AE＝AC ， 连接DE ， 已知DE＝2cm ， BD＝3cm ． 求：
(1)、线段BC的长；(2)、若∠ACB的平分线CF交AD于点O ， 且O到AC的距离是acm ， 请补充图形，并用含a的代数式表示△ABC的面积．28. 如图，已知在△ABC中，∠BAC为直角，AB＝AC，D为AC上一点，CE⊥BD于E，交BA的延长线于F.
(1)、求证：△ABD≌△ACF；(2)、若BD平分∠ABC，求证：CE＝ BD；(3)、若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，直接写出它的度数.