初数浙教版九上二次函数图象与坐标轴的交点问题 专项复习(困难版)
试卷更新日期:2021-12-16 类型:复习试卷
一、单选题
-
1. 如图,已知抛物线l:y= (x-2)2-2与x轴分别交于0、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果山抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
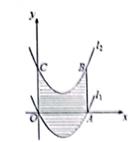 A、y= (x-2)2+4 B、y= (x-2)2+3 C、y= (x-2)2+2 D、y= (x-2)2+12. 已知二次函数y=ax2+bx+c的部分图象如图所示,当y>0时,x的取值范围是( )
A、y= (x-2)2+4 B、y= (x-2)2+3 C、y= (x-2)2+2 D、y= (x-2)2+12. 已知二次函数y=ax2+bx+c的部分图象如图所示,当y>0时,x的取值范围是( )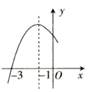 A、x>-3 B、-3<x<1 C、x<-3或x>1 D、x<13. 如图,抛物线 y=ax2+bx+c ,下列结论:① a>0 ;② b2-4ac >0;③4a+b=0 ;④不等式ax2+(b-1)x+c<0的解集为1<x<3,正确的结论个数是( )
A、x>-3 B、-3<x<1 C、x<-3或x>1 D、x<13. 如图,抛物线 y=ax2+bx+c ,下列结论:① a>0 ;② b2-4ac >0;③4a+b=0 ;④不等式ax2+(b-1)x+c<0的解集为1<x<3,正确的结论个数是( )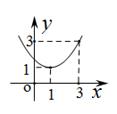 A、1 B、2 C、3 D、44. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点5. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、1 B、2 C、3 D、44. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点5. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )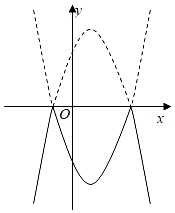 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣36. 在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数 的图象在 轴上方的部分与 轴围成的区域(不含边界)为 .例如当 时,区域 内的整点个数为1,若区域 内恰有7个整点,则 的取值范围是( )A、 B、 C、 D、7. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、8. 如图,抛物线 与 轴交于点 ,与 轴的负半轴交于点 ,点 是对称轴上的一个动点.连接 ,当 最大时,点 的坐标是( )
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣36. 在平面直角坐标系中,横、纵坐标都是整数的点叫做整点,记函数 的图象在 轴上方的部分与 轴围成的区域(不含边界)为 .例如当 时,区域 内的整点个数为1,若区域 内恰有7个整点,则 的取值范围是( )A、 B、 C、 D、7. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、8. 如图,抛物线 与 轴交于点 ,与 轴的负半轴交于点 ,点 是对称轴上的一个动点.连接 ,当 最大时,点 的坐标是( )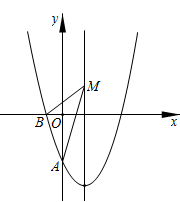 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
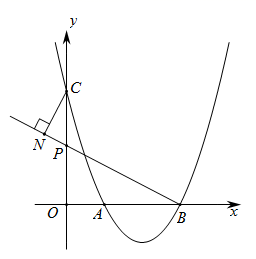
9. 若抛物线y=x2﹣x﹣k与x轴的两个交点都在x轴正半轴上,则k的取值范围是 .10. 抛物线 与 的一个交点坐标是 ,则另一个交点坐标是 .11. 抛物线y=x2﹣x﹣1与x轴的一个交点的坐标为(m , 0),则代数式m2﹣m+2021= .12. 如图,抛物线 过点A(1,0),B(3,0),与y轴相交于点C.若点P为线段OC上的动点,连结BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,点N运动路径的长为
 13. 如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是.
13. 如图,抛物线y=﹣x2+4x﹣3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是.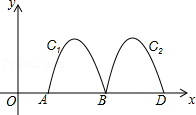 14. 如图,直线l: ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若其中一条抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这条抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时能产生美丽抛物线相应的d的值是.
14. 如图,直线l: ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若其中一条抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这条抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时能产生美丽抛物线相应的d的值是.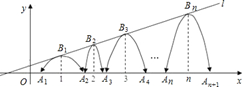
三、解答题
-
15. 已知抛物线y=x2+bx+c的图象如图所示,它与x轴的一个交点的坐标为A(﹣1,0),与y轴的交点坐标为C(0,﹣3).
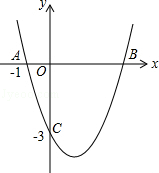 (1)、求抛物线的解析式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,y<0?(3)、在抛物线的对称轴上有一动点P,求PA+PB的值最小时的点P的坐标.16. 已知二次函数 的图象与x轴交于 两点,且 ,求a的值.17. 如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)、求抛物线的解析式及与x轴的另一个交点B的坐标;(2)、根据图象回答:当x取何值时,y<0?(3)、在抛物线的对称轴上有一动点P,求PA+PB的值最小时的点P的坐标.16. 已知二次函数 的图象与x轴交于 两点,且 ,求a的值.17. 如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C. (1)、求抛物线的函数解析式;(2)、求△ABC的面积;(3)、能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.18. 在平面直角坐标系xOy中,已知抛物线的对称轴是 , 并且经过点(-2,-5).
(1)、求抛物线的函数解析式;(2)、求△ABC的面积;(3)、能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.18. 在平面直角坐标系xOy中,已知抛物线的对称轴是 , 并且经过点(-2,-5).
(1)求此抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,D是线段BC上一点(不与点B、C重合), 若以B、O、D为顶点的三角形与△BAC相似,求点D的坐标;
(3)点P在y轴上,点M在此抛物线上,若要使以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.19. 如图1,在平面直角坐标系中,二次函数y=﹣x2+12的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.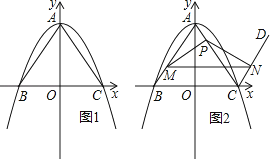
(1)点B的坐标为 , 点C的坐标为 ;
(2)过点C作射线CD∥AB,点M是线段AB上的动点,点P是线段AC上的动点,且始终满足BM=AP(点M不与点A,点B重合),过点M作MN∥BC分别交AC于点Q,交射线CD于点N (点 Q不与点P重合),连接PM,PN,设线段AP的长为n.
①如图2,当n<AC时,求证:△PAM≌△NCP;
②直接用含n的代数式表示线段PQ的长;
③若PM的长为 , 当二次函数y=﹣x2+12的图象经过平移同时过点P和点N时,请直接写出此时的二次函数表达式.