2022年浙江省中考专项复习3 一元一次方程及其运用

试卷更新日期：2021-12-16 类型：一轮复习

进入出卷网下载

一、单选题

1. 若x＝ $\frac{2}{3}$ 是关于x的方程3x﹣a＝0的解，则a的值为（）

A、﹣2 B、 $\frac{1}{2}$ C、2 D、- $\frac{1}{2}$

查看试题解析
2. 下列等式中是一元一次方程的是（　　）

A、 $x = 0.5$ B、 $x - y = 0$ C、 $\frac{1}{x} = 1$ D、 $3 - 2 = 1$

查看试题解析
3. 若a=b，则下列各式不一定成立的是（）

A、a－1=b－1 B、 $\frac{a}{2} = \frac{b}{2}$ C、－a=－b D、 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
4. 下列变形中，正确的是（）

A、x﹣（z﹣y）＝x﹣z﹣y B、如果x＝y，那么 $\frac{x}{m} = \frac{y}{m}$ C、x﹣y+z＝x﹣（y﹣z） D、如果|x|＝|y|，那么x＝y

查看试题解析
5. 若（m﹣2）x^|^m^﹣³^|=4是一元一次方程，则m的值是（）

A、4或2 B、2 C、4 D、﹣4

查看试题解析
6. 足球比赛的积分规则：胜一场得3分，平一场得1分，负一场得0分．一个队进行了14场比赛，其中负5场，共得19分，那么这个对共胜了（）场．

A、3 B、4 C、5 D、6

查看试题解析
7. （古代数学问题）今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？意思是：几个人一起去买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？设有x人，则根据题意列出方程正确的是（）

A、8x+3=7x﹣4 B、8x﹣3=7x+4 C、8x﹣3=7x﹣4 D、8x+3=7x+4

查看试题解析
8. 七年级学生在参加校外实践活动中，有m位师生乘坐n辆客车．若每辆客车乘42人，则还有8人不能上车，若每辆客车乘45人，则最后一辆车空了16个座位．在下列四个方程：①42n－8＝45n＋16；② $\frac{m + 8}{42}$ ＝ $\frac{m - 16}{45}$ ；③ $\frac{m - 8}{42}$ ＝ $\frac{m + 16}{45}$ ；④42n＋8＝45n－16中，其中正确的有（）

A、①③ B、②④ C、①④ D、③④

查看试题解析

9. 佳佳坐在匀速行驶的车上，将每隔一段时间看到的里程碑上的数描述如下：

时刻	12：00	13：00	14：00
里程碑上的数	是一个两位数，数字之和为7	十位数字与个位数字相比12：00时看到的刚好颠倒	比12：00看到的两位数中间多了个0

则12：00时看到的两位数是（）

A、16 B、25 C、34． D、52

查看试题解析

10. 某超市推出如下优惠方案：（1）一次性购物不超过100元不享受优惠；（2）一次性购物超过100元，但不超过300元一律九折；（3）一次性购物超过300元一律八折；兰兰两次购物分别付款80元，252元．如果兰兰一次性购买和上两次相同的物品应付款（）

A、288元 B、288元和332元 C、332元 D、288元和316元

查看试题解析

二、填空题

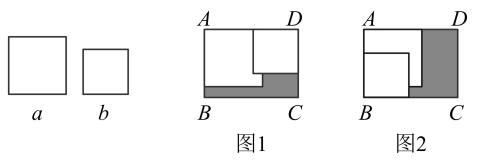
11. 三个连续偶数的和为零，它们是．

查看试题解析
12. 用方程表示“x的 $\frac{1}{3}$ 与 $\frac{1}{2}$ 的和是6”是．

查看试题解析
13. 已知关于x的一元一次方程 $3 x = 2 x + m$ 的解为 $x = - 3$ ，则m的值为．

查看试题解析
14. 若代数式1﹣8x与9x﹣3的值互为相反数，则x＝.

查看试题解析
15. 已知关于x的方程 $\frac{2 a - 1}{3} - 2 x = 1$ 的解是 $x = - 2$ ，则a的值为．

查看试题解析
16. 某超市推出如下优惠方案：⑴ 一次性购物不超过100元不享受优惠； ⑵ 一次性购物超过100元但不超过300元一律9折； ⑶一次性购物超过300元一律8折。某人两次购物分别付款99元和252元，如果该人一次性购买以上两次相同的商品，则应付元。（注：9折是指折后价格为原来的90%）

查看试题解析
17. 甲乙二人在环形跑道上同时同地出发，同向运动，若甲的速度是乙的速度的2倍，则乙运动1周，甲、乙第一次相遇；若甲的速度是乙的速度的3倍，则乙运动 $\frac{1}{2}$ 周，甲、乙第一次相遇；若甲的速度是乙的速度的4倍，则乙运动 $\frac{1}{3}$ 周，甲、乙第一次相遇；……以此探究正常走时的时钟，时针和分针从重叠位置同时出发，时针旋转周，时针和分针第一次相遇.

查看试题解析
18. 已知长方形ABCD，AD>AB，AD=10，将两张边长分别为a和b（a>b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S₁ ，图2中阴影部分的面积为S₂ ，当S₂-S₁=3b时，AB=。

查看试题解析

三、计算题

19. 解方程：

(1)、 $4 (x - 1) = 1 - x$ ；

(2)、 $\frac{x - 1}{2} - 1 = \frac{x - 5}{3}$ .

查看试题解析

四、综合题

20. 为了备战学校体育节的乒乓球比赛活动，某班计划买5副乒乓球拍和若干盒乒乓球（多于5盒）．该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球，乒乓球拍每副售价100元，乒乓球每盒售价25元．经过体育委员的洽谈，甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠；乙商店给出乒乓球拍和乒乓球全部九折的优惠．

(1)、若这个班计划购买6盒乒乓球，则在甲商店付款元，在乙商店付款元；

(2)、当这个班购买多少盒乒乓球时，在甲、乙两家商店付款相同？

查看试题解析
21. 下表是某网约车公司的专车计价规则

计费项目

起租价

里程费

时长费

单价

10元

2.5元/千米

1元/分

注：应付车费＝起租价＋里程费＋时长费，其中起租价10元含5千米里程费和10分钟时长费.

例如：若坐专车行驶里程为12千米，行车时间为20分钟，则需付车费：

$10 + 2.5 \times (12 - 5) + 1 \times (20 - 10) = 37.5$ （元）.

若坐专车行驶里程为4千米，行车时间为12分钟，则需付车费： $10 + 1 \times (12 - 10) = 12$ （元）.

(1)、若小聪乘坐专车，行车里程为20千米，行车时间为30分，则需付车费元；

(2)、若小聪乘坐专车，行车里程为 $x$ （ $7 < x \leq 10$ ）千米，平均时速为40千米/时，则小聪应付车费多少元？（用含 $x$ 的代数式表示）

(3)、小聪与小明各自乘坐专车从家去吾悦广场，由于堵车，小聪乘坐了12分钟，小明乘坐了20分钟，两车车费之和为47元，里程之和为15千米（其中小聪的行车里程不超过5千米）.那么这两辆专车此次的行驶路程各为多少千米？

查看试题解析

22. 某市居民使用自来水按如下标准收费（水费按月缴纳）

户月用水量	单价
不超过12 m³的部分	2元/m³
超过12 m³但不超过20 m³的部分	3元/m³
超过20 m³的部分	4元/m³

(1)、某用户一个月用了14 m³水，求该用户这个月应缴纳的水费

(2)、某户月用水量为n立方米（12＜n≤20），该用户缴纳的水费是39元，列方程求n的值

(3)、甲、乙两用户一个月共用水40 m³ ，设甲用户用水量为x m³ ，且12＜x≤28

① 当12＜x≤20时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）

② 当20＜x≤28时，甲、乙两用户一个月共缴纳的水费为元（用含x的整式表示）

查看试题解析

23. 以下是两张不同类型火车的车票：（“D×××次”表示动车，“G×××次”表示高铁）：

(1)、根据车票中的信息填空：两车行驶方向，出发时刻（填“相同”或“不同”）；

(2)、已知该动车和高铁的平均速度分别为200km/h ， 300km/h ，如果两车均按车票信息准时出发，且同时到达终点，求A ， B两地之间的距离；

(3)、在（2）的条件下，请求出在什么时刻两车相距100km？

查看试题解析

计费项目	起租价	里程费	时长费
单价	10元	2.5元/千米	1元/分