贵州省铜仁市玉屏侗族自治县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
1. 2的相反数是( )A、 B、 C、2 D、-22. 下列计算正确的是( )A、 B、 C、 D、3. 如图,直线 , ,则 的度数为( ).
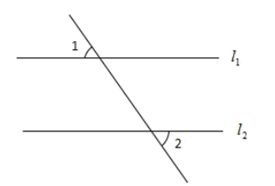 A、 B、 C、 D、4. 已知关于x的一元二次方程 ,下列说法正确的是( )A、方程有两个相等是实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定5. 我国是世界上严重缺水的国家之一,目前我国可利用的淡水资源总量为27500亿 ,人均占有淡水量居全世界第110位,因此我们要节约用水.27500亿这个数用科学记数法表示为( )A、 B、 C、 D、6. 如果一个多边形的每一个外角都是 ,则这个多边形的边数是( )A、6 B、8 C、10 D、127. 在一次数学模拟考试中,小明所在学习小组7名同学的成绩分别为:130,135,145,135,148,135,152,则这次考试的平均数和众数分别为( )A、145,135 B、140,135 C、136,148 D、136,1458. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、
A、 B、 C、 D、4. 已知关于x的一元二次方程 ,下列说法正确的是( )A、方程有两个相等是实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定5. 我国是世界上严重缺水的国家之一,目前我国可利用的淡水资源总量为27500亿 ,人均占有淡水量居全世界第110位,因此我们要节约用水.27500亿这个数用科学记数法表示为( )A、 B、 C、 D、6. 如果一个多边形的每一个外角都是 ,则这个多边形的边数是( )A、6 B、8 C、10 D、127. 在一次数学模拟考试中,小明所在学习小组7名同学的成绩分别为:130,135,145,135,148,135,152,则这次考试的平均数和众数分别为( )A、145,135 B、140,135 C、136,148 D、136,1458. 若 ,则正比例函数 与反比例函数 在同一坐标系中的大致图象可能是( )A、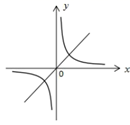 B、
B、 C、
C、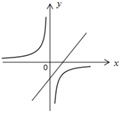 D、
D、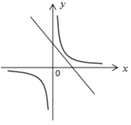 9. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )
9. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )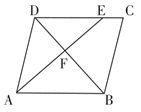 A、4:1 B、16:5 C、16:25 D、5:410. 如图,直线 与x轴交于点A,与y轴交于点C,与反比例函数 在第一象限内的图象交于点B,连接 ,若 ,则 的值是( )
A、4:1 B、16:5 C、16:25 D、5:410. 如图,直线 与x轴交于点A,与y轴交于点C,与反比例函数 在第一象限内的图象交于点B,连接 ,若 ,则 的值是( )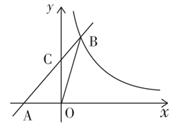 A、1、-3 B、1、3 C、2、3 D、3、-1
A、1、-3 B、1、3 C、2、3 D、3、-1二、填空题
-
11. |-3| =
12. 方程 的解是.13. 为使 有意义,则x的取值范围是.14. 已知点 关于x轴的对称点为 ,则 .15. 如果菱形的两条对角线长分别是 和 那么这个菱形的面积为 .16. 如图,某住宅小区在施工过程中留下了一块空地四边形 ,经测量, , , , , .小区美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地需花元.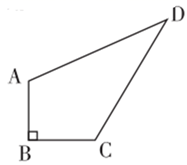 17. 将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,……,依次类推,第行最后一个数是2020.
17. 将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,……,依次类推,第行最后一个数是2020.
三、解答题
-
18.(1)、计算:(2)、已知 ,先化简,再求 的值.19. 网瘾低龄化问题已引起社会各界的高度关注,特别是手机上网.有关部门在全国范围内对12-35岁的网瘾人群进行了简单随机抽样调查并得到统计图,其中30-35岁的网瘾人数占样本总人数的 .
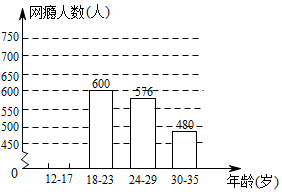 (1)、请把图中缺失的数据、图形补充完整.(2)、据报道,目前我国12-35岁网瘾人数约2000万人,请你根据图中数据估计我国目前12-35岁的网瘾人群中12-17岁的网瘾人数.(3)、作为初中生的你,应如何正确对待网络?20. 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)、请把图中缺失的数据、图形补充完整.(2)、据报道,目前我国12-35岁网瘾人数约2000万人,请你根据图中数据估计我国目前12-35岁的网瘾人群中12-17岁的网瘾人数.(3)、作为初中生的你,应如何正确对待网络?20. 如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.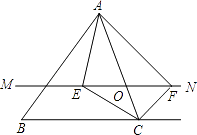 (1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论.21. 如图,水库大坝的横断面是梯形,坝顶 ,坝高 ,斜坡 的坡度 ,求坝底 的长.( ,结果精确到 )
(1)、求证:EO=FO;(2)、当点O运动到何处时,四边形AECF是矩形?并证明你的结论.21. 如图,水库大坝的横断面是梯形,坝顶 ,坝高 ,斜坡 的坡度 ,求坝底 的长.( ,结果精确到 ) 22. 某箫笛厂设计了一款成本为10元/根的箫笛,并投放市场进行试销.经过调查,发现每天的销售量y(件)与销售单价x(元)存在一次函数关系 .(1)、销售单价定为多少时,该厂每天获取的利润最大?最大利润为多少?(2)、若物价部门规定,该产品的最高销售价不得超过38元/根,那么销售单价如何定位才能获取最大利润?23. 如图,正方形 的边长是4, ,线段 的两端点在 上滑动,当 为多长时, 与以D,M,N为顶点的三角形相似?请说明理由.
22. 某箫笛厂设计了一款成本为10元/根的箫笛,并投放市场进行试销.经过调查,发现每天的销售量y(件)与销售单价x(元)存在一次函数关系 .(1)、销售单价定为多少时,该厂每天获取的利润最大?最大利润为多少?(2)、若物价部门规定,该产品的最高销售价不得超过38元/根,那么销售单价如何定位才能获取最大利润?23. 如图,正方形 的边长是4, ,线段 的两端点在 上滑动,当 为多长时, 与以D,M,N为顶点的三角形相似?请说明理由.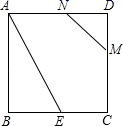 24. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D.
24. 如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.
(1)、求二次函数的表达式.(2)、在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.(3)、有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.