贵州省铜仁市松桃苗族自治县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
1. 下列各点中,在反比例函数 图象上点的坐标是( )A、 B、 C、 D、2. 下列一元二次方程没有实数根的是( )A、 B、 C、 D、3. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
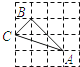 A、
A、 B、
B、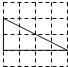 C、
C、 D、
D、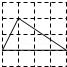 4. 二次函数 的图象顶点坐标为( )A、(1,1) B、(1,-1) C、(-1,1) D、(-1,-1)5. 一元二次方程 的解是( )A、 B、 C、 D、6. 如图, 是 以点 为位似中心经过位似变换得到的,若 与 的周长比是 ,则它们的面积比为( )
4. 二次函数 的图象顶点坐标为( )A、(1,1) B、(1,-1) C、(-1,1) D、(-1,-1)5. 一元二次方程 的解是( )A、 B、 C、 D、6. 如图, 是 以点 为位似中心经过位似变换得到的,若 与 的周长比是 ,则它们的面积比为( ) A、 B、 C、 D、7. 某学校准备修建一个面积为200平方米的矩形花圃,它的长比宽多10米,设花圃的宽为x米,则可列方程为( )A、x(x-10)=200 B、2x+2(x-10)=200 C、x(x+10)=200 D、2x+2(x+10)=2008. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( )
A、 B、 C、 D、7. 某学校准备修建一个面积为200平方米的矩形花圃,它的长比宽多10米,设花圃的宽为x米,则可列方程为( )A、x(x-10)=200 B、2x+2(x-10)=200 C、x(x+10)=200 D、2x+2(x+10)=2008. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC= ,BC=2,则sin∠ACD的值为( ) A、 B、 C、 D、9. 如图,函数y1=x﹣1和函数 的图象相交于点M(2,m),N(﹣1,n),若y1>y2 , 则x的取值范围是( )
A、 B、 C、 D、9. 如图,函数y1=x﹣1和函数 的图象相交于点M(2,m),N(﹣1,n),若y1>y2 , 则x的取值范围是( ) A、x<﹣1或0<x<2 B、x<﹣1或x>2 C、﹣1<x<0或0<x<2 D、﹣1<x<0或x>210. 如图,点 在线段 上,在 的同侧作等腰直角三角形 和等腰直角三角形 ( 和 是直角),连接 交于点 与 边交于点 ,对于下列结论:① ,② ,③ ,④ ,其中正确的个数为( )
A、x<﹣1或0<x<2 B、x<﹣1或x>2 C、﹣1<x<0或0<x<2 D、﹣1<x<0或x>210. 如图,点 在线段 上,在 的同侧作等腰直角三角形 和等腰直角三角形 ( 和 是直角),连接 交于点 与 边交于点 ,对于下列结论:① ,② ,③ ,④ ,其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若反比例函数 的图象在第二、四象限,则m的取值范围是.12. 若2是关于方程 的一个根,则这个方程的另一个根是 .13. 如果某商品原销售价为 元,经过连续两次涨价后销售价上升为 元,那么平均每次增长的百分率为.14. 一组数据:2,3,4,2,4的方差是.15. 如图,身高1.6米的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是米.
 16. 如图,点 是反比例函数 的图象上任意一点,过点 作 轴,垂足为点 ,点 在 轴上,若 的面积等于 ,则 的值等于.
16. 如图,点 是反比例函数 的图象上任意一点,过点 作 轴,垂足为点 ,点 在 轴上,若 的面积等于 ,则 的值等于. 17. 如图,在 中, ,正方形 的顶点 分别在 的边上, 在 边上,则正方形 的边长等于.
17. 如图,在 中, ,正方形 的顶点 分别在 的边上, 在 边上,则正方形 的边长等于. 18. 已知, , 则 .
18. 已知, , 则 .三、解答题
-
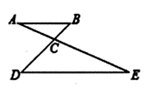
19.(1)、计算:(2)、解方程:20. 如图, 与 相交于点 ,已知 , , , .求证: .
 21. 某校对本校的5000名学生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
21. 某校对本校的5000名学生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:视力
频数(人)
20
0.1
40
0.2
70
0.35
0.3
10
 (1)、在频数分布表中, 的值为 , 的值为 , 将频数分布直方图补充完整;(2)、小明说“我的视力情况是此次抽样调查所得数据的中位数”小明的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,请估计该校学生中视力正常的大约有多少人?22. 为了方便市民出行,县政府决定从“七星广场”河堤到对岸修建一座便民桥.为测量河的宽度,在河的对岸取一点 ,在广场河边取两点 测得点 在点 的北偏东 方向,测得点 在点 北偏东 方向,量得 长为 米,求河的宽度 (结果保留根号)
(1)、在频数分布表中, 的值为 , 的值为 , 将频数分布直方图补充完整;(2)、小明说“我的视力情况是此次抽样调查所得数据的中位数”小明的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,请估计该校学生中视力正常的大约有多少人?22. 为了方便市民出行,县政府决定从“七星广场”河堤到对岸修建一座便民桥.为测量河的宽度,在河的对岸取一点 ,在广场河边取两点 测得点 在点 的北偏东 方向,测得点 在点 北偏东 方向,量得 长为 米,求河的宽度 (结果保留根号) 23. 某工艺厂设计了一款成本为每件30元的产品,并投放市场进行试销,经过调查,发现每天的销售数量 件与销售单价 (元)存在一次函数关系(1)、要使每天销售利润达到600元,销售单价应定为每件多少元?(2)、销售单价定为多少时,该厂每天获取的利润最大?最大利润是多少?
23. 某工艺厂设计了一款成本为每件30元的产品,并投放市场进行试销,经过调查,发现每天的销售数量 件与销售单价 (元)存在一次函数关系(1)、要使每天销售利润达到600元,销售单价应定为每件多少元?(2)、销售单价定为多少时,该厂每天获取的利润最大?最大利润是多少?

