贵州省毕节市织金县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
1. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣32. 反比例函数y= 的图象经过点(3,﹣2),下列各点在图象上的是( )
A、(﹣3,﹣2) B、(3,2) C、(﹣2,﹣3) D、(﹣2,3)3. 在 中, , , ,则 等于( )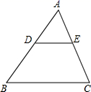 A、10 B、8 C、9 D、64. 如图,小明居住的小区内有一条笔直的小路,有一盏路灯位于小路上 两点的正中间,晚上,小明由点 处径直走到点 处,他在灯光照射下的影长 与行走路程 之间的变化关系用图象表示大致是( )
A、10 B、8 C、9 D、64. 如图,小明居住的小区内有一条笔直的小路,有一盏路灯位于小路上 两点的正中间,晚上,小明由点 处径直走到点 处,他在灯光照射下的影长 与行走路程 之间的变化关系用图象表示大致是( )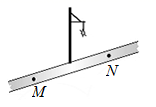 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、菱形的面积等于对角线乘积的一半 D、对角线互相垂直平分的四边形是正方形6. 关于 的一元二次方程 有实数根,则 满足( )A、 B、 且 C、 且 D、7. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
5. 下列说法中不正确的是( )A、对角线垂直的平行四边形是菱形 B、对角线相等的平行四边形是矩形 C、菱形的面积等于对角线乘积的一半 D、对角线互相垂直平分的四边形是正方形6. 关于 的一元二次方程 有实数根,则 满足( )A、 B、 且 C、 且 D、7. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( ) A、24 B、18 C、12 D、98. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A、24 B、18 C、12 D、98. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )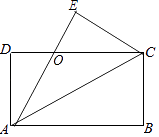 A、6cm B、7cm C、8cm D、9cm9. 如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段 AC 的长为( )
A、6cm B、7cm C、8cm D、9cm9. 如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段 AC 的长为( )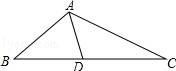 A、4 B、4 C、6 D、410. 桌面上放置的几何体中,主视图与左视图可能不同的是( )A、圆柱 B、正方体 C、球 D、直立圆锥11. 某商品的售价为100元,连续两次降价 后售价降低了36元,则 的值为( )A、60 B、20 C、36 D、1812. 已知点 (-2, ), (3, )是反比例函数 图象上的两点,则有( )A、 B、 C、 D、13. 在平面直角坐标系中,线段 两个端点的坐标分别为 .若以原点 为位似中心,在第三象限内将线段 扩大为原来的2倍得到线段 ,则点 的对应点 的坐标为( )A、 B、 C、 D、14. 如图,直线 与坐标轴分别交于点 ,与若双曲线 交于点 ,则 为( )
A、4 B、4 C、6 D、410. 桌面上放置的几何体中,主视图与左视图可能不同的是( )A、圆柱 B、正方体 C、球 D、直立圆锥11. 某商品的售价为100元,连续两次降价 后售价降低了36元,则 的值为( )A、60 B、20 C、36 D、1812. 已知点 (-2, ), (3, )是反比例函数 图象上的两点,则有( )A、 B、 C、 D、13. 在平面直角坐标系中,线段 两个端点的坐标分别为 .若以原点 为位似中心,在第三象限内将线段 扩大为原来的2倍得到线段 ,则点 的对应点 的坐标为( )A、 B、 C、 D、14. 如图,直线 与坐标轴分别交于点 ,与若双曲线 交于点 ,则 为( )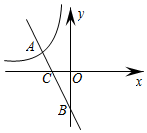 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 若一元二次方程 的两根为 ,则 的值为.16. 如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在B处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AB=2米,BC=18米,则旗杆CD的高度是米.
 17. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .18. 如图,点A在双曲线 上,过点A作 轴,垂足为C,OA的垂直平分线交OC于点B,当 时, 的周长为.
17. 菱形的两条对角线长分别是方程 的两实根,则菱形的面积为 .18. 如图,点A在双曲线 上,过点A作 轴,垂足为C,OA的垂直平分线交OC于点B,当 时, 的周长为. 19. 如图, 分别是 的边 上的点, ,若 ,则 .
19. 如图, 分别是 的边 上的点, ,若 ,则 .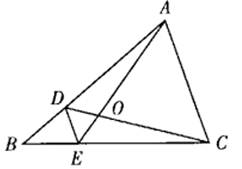
三、解答题
-
20. 解方程(1)、(2)、21. 四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
 (1)、求证:△ADE≌△ABF;(2)、填空:△ABF可以由△ADE绕旋转中心点,按顺时针方向旋转度得到;(3)、若BC=8,DE=6,求△AEF的面积.22. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高 的小明( )落在地面上的影长 .
(1)、求证:△ADE≌△ABF;(2)、填空:△ABF可以由△ADE绕旋转中心点,按顺时针方向旋转度得到;(3)、若BC=8,DE=6,求△AEF的面积.22. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高 的小明( )落在地面上的影长 .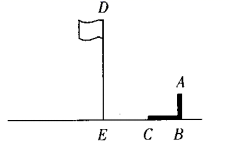 (1)、请画出旗杆 在同一时刻阳光照射下在地面上的影子 .(2)、若小明测得此刻旗杆落在地面上的影长 ,求旗杆 的高度.23. 为增强学生环保意识,某中学举办了环保知识竞赛,某班共有5名学生(3名男生,2名女生)获奖.(1)、老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为.(2)、老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.24. 如图,已知 是 斜边上的中线,过 作 的平行线,过点 作 垂线,两线相交于点 .
(1)、请画出旗杆 在同一时刻阳光照射下在地面上的影子 .(2)、若小明测得此刻旗杆落在地面上的影长 ,求旗杆 的高度.23. 为增强学生环保意识,某中学举办了环保知识竞赛,某班共有5名学生(3名男生,2名女生)获奖.(1)、老师若从获奖的5名学生中选取一名作为班级的“环保小卫士”,则恰好是男生的概率为.(2)、老师若从获奖的5名学生中任选两名作为班级的“环保小卫士”,请用画树状图法或列表法,求出恰好是一名男生、一名女生的概率.24. 如图,已知 是 斜边上的中线,过 作 的平行线,过点 作 垂线,两线相交于点 .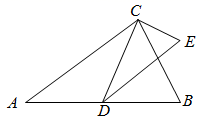 (1)、求证: ;(2)、若 ,求线段 的长.25. 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润为10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)、求证: ;(2)、若 ,求线段 的长.25. 某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润为10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.
(1)、若生产的某批次蛋糕每件利润为14元,此批次蛋糕属于第几档次产品?
(2)、由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?26. 如图,一次函数 的图象与反比例函数 的图象交于 两点,与 交于点 ,点 的坐标为 .点 的坐标为 ,连接 . (1)、求一次函数 与反比例函数 的表达式;(2)、求 点坐标和 的面积;(3)、直接写出 时自变量 的取值范围.
(1)、求一次函数 与反比例函数 的表达式;(2)、求 点坐标和 的面积;(3)、直接写出 时自变量 的取值范围.