贵州省安顺市关岭布依族苗族自治县2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
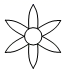 B、
B、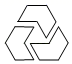 C、
C、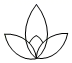 D、
D、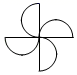 2. 下列说法中,正确的是( )A、打开电视,正在播放电视剧《隐秘而伟大》是必然事件 B、“若m,n互为相反数,则 ”,这一事件是随机事件 C、“1,3,2,1的中位数一定是2”,这一事件是不可能事件 D、“广安市明天降雨的概率是80%”,意思是广安市明天有80%的时间在降雨3. 如图,若 绕点A沿逆时针方向旋转56°后与 重合,则 的度数为( )
2. 下列说法中,正确的是( )A、打开电视,正在播放电视剧《隐秘而伟大》是必然事件 B、“若m,n互为相反数,则 ”,这一事件是随机事件 C、“1,3,2,1的中位数一定是2”,这一事件是不可能事件 D、“广安市明天降雨的概率是80%”,意思是广安市明天有80%的时间在降雨3. 如图,若 绕点A沿逆时针方向旋转56°后与 重合,则 的度数为( ) A、62° B、60° C、56° D、34°4. 如图,四边形ABCD为 的内接四边形, ,则 的度数为( )
A、62° B、60° C、56° D、34°4. 如图,四边形ABCD为 的内接四边形, ,则 的度数为( ) A、48° B、96° C、132° D、144°5. 若关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是( )A、 B、 C、 且 D、6. 将抛物线 的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函数解析式是( )A、 B、 C、 D、7. 若 是一元二次方程 的两个实数根,则 的值为( )A、2020 B、2019 C、2018 D、20178. 如图,在平面直角坐标系中,点 的坐标分别为 和 ,月牙绕点B旋转 得到新的月牙,则点A的对应点 的坐标是( )
A、48° B、96° C、132° D、144°5. 若关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是( )A、 B、 C、 且 D、6. 将抛物线 的图象向右平移2个单位长度,再向下平移4个单位长度,所得的抛物线的函数解析式是( )A、 B、 C、 D、7. 若 是一元二次方程 的两个实数根,则 的值为( )A、2020 B、2019 C、2018 D、20178. 如图,在平面直角坐标系中,点 的坐标分别为 和 ,月牙绕点B旋转 得到新的月牙,则点A的对应点 的坐标是( ) A、 或 B、 或 C、 或 D、 或9. 往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽 ,则水的最大深度为( )
A、 或 B、 或 C、 或 D、 或9. 往直径为26cm的圆柱形容器内装入一些水以后,截面如图所示.若水面宽 ,则水的最大深度为( ) A、4cm B、5cm C、8cm D、10cm10. 如图,二次函数 的图象经过点( ,0),对称轴为直线 ,给出下列结论:① ;② ;③ ;④ ;⑤ .其中正确的结论有( )
A、4cm B、5cm C、8cm D、10cm10. 如图,二次函数 的图象经过点( ,0),对称轴为直线 ,给出下列结论:① ;② ;③ ;④ ;⑤ .其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在一个不透明的布袋中装有红球、白球共20个,它们除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红球的频率稳定在0.6,则随机从布袋中摸出一个球是红球的概率是.12. 如图,正方形 的边长为6,点 在边 上.以点 为中心,把 顺时针旋转 至 的位置,若 ,则 .
 13. 已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为.
13. 已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为. 14. 已知圆锥的侧面展开图的面积是 ,圆心角是60°,则这个圆锥的底面圆的半径是 .15. 如图,MN为 的直径,⊙O的半径为3,点A在 上, ,B为 的中点,P是直径MN上一动点,则 的最小值为.
14. 已知圆锥的侧面展开图的面积是 ,圆心角是60°,则这个圆锥的底面圆的半径是 .15. 如图,MN为 的直径,⊙O的半径为3,点A在 上, ,B为 的中点,P是直径MN上一动点,则 的最小值为.
三、解答题
-
16. 解下列方程:(1)、 ;(2)、 .17. 如图,在平面直角坐标系中, 三个顶点的坐标分别是 .

( 1 )作出 关于点O对称的图形 ;
( 2 )以点O为旋转中心,将 顺时针旋转 ,得 ,在坐标系中画出 ,并写出点 的坐标.
18. 如图,AB是 的直径,弦 于点E,G是 上的点,AG,DC的延长线交于点F. (1)、求证: ;(2)、若 , ,求AD的长.19. “绿水青山就是金山银山”,为加快城乡绿化建设,某市2018年的绿化面积约1200万平方米,预计2020年的绿化面积约1587万平方米.假设每年绿化面积的平均增长率相同.(1)、求每年绿化面积的平均增长率.(2)、若2021年的绿化面积继续保持相同的增长率,那么2021年的绿化面积是多少?20. 某河上有抛物线形拱桥,当水面离拱顶5m时,水面宽8m.一木船宽4m,高2m,载货后,木船露出水面的部分为 m.以拱顶O为坐标原点建立如图所示的平面直角坐标系,A、B为抛物线与水面的交点.
(1)、求证: ;(2)、若 , ,求AD的长.19. “绿水青山就是金山银山”,为加快城乡绿化建设,某市2018年的绿化面积约1200万平方米,预计2020年的绿化面积约1587万平方米.假设每年绿化面积的平均增长率相同.(1)、求每年绿化面积的平均增长率.(2)、若2021年的绿化面积继续保持相同的增长率,那么2021年的绿化面积是多少?20. 某河上有抛物线形拱桥,当水面离拱顶5m时,水面宽8m.一木船宽4m,高2m,载货后,木船露出水面的部分为 m.以拱顶O为坐标原点建立如图所示的平面直角坐标系,A、B为抛物线与水面的交点. (1)、B点的坐标为;(2)、求抛物线解析式;(3)、当水面离拱顶1.8米时,木船能否通过拱桥?21. 某中学为了解九年级学生对足球、篮球、排球这三种球类运动的喜爱情况,从九年级学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制了如下两幅尚不完整的统计图.
(1)、B点的坐标为;(2)、求抛物线解析式;(3)、当水面离拱顶1.8米时,木船能否通过拱桥?21. 某中学为了解九年级学生对足球、篮球、排球这三种球类运动的喜爱情况,从九年级学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制了如下两幅尚不完整的统计图.
请根据两幅统计图中的信息解答下列问题:
(1)、求此次调查的学生总人数,并补全条形统计图.(2)、若该中学九年级共有500名学生,请你估计该中学九年级学生中喜爱篮球运动的学生有多少人?(3)、若从喜爱足球运动的2名男生和2名女生中随机抽取两名学生,确定为该校足球运动员的重点培养对象,请用列表或画树状图的方法求抽取的两名学生恰好为1名男生和1名女生的概率.22. 某超市销售一种文具,进价为5元/件.在销售过程中发现,当售价为6元/件时,日销售量为100件,每件售价每上涨0.5元,日销售量就减少5件.设每件文具的售价为x元/件时( ,且x是按0.5元的倍数上涨),日销售利润为y元.(1)、求y与x的函数关系式.(不要求写出自变量的取值范围)(2)、若每件文具的利润不超过 ,要想获得最大日销售利润,每件文具的售价应为多少元?并求出最大利润.23. 如图,在 中, 是直角边 所在直线上的一个动点,连接 ,将 绕点A逆时针旋转 到 ,连接 . (1)、如图1,当点E恰好在线段 上时,请判断线段 和 之间的数量关系,并说明理由.(2)、当点E不在直线 上时,如图2、图3,其他条件不变,(1)中结论是否成立?若成立,请在图2、图3中选择一个给予证明;若不成立,请直接写出 和 之间的数量关系.
(1)、如图1,当点E恰好在线段 上时,请判断线段 和 之间的数量关系,并说明理由.(2)、当点E不在直线 上时,如图2、图3,其他条件不变,(1)中结论是否成立?若成立,请在图2、图3中选择一个给予证明;若不成立,请直接写出 和 之间的数量关系.

