甘肃省兰州市教学管理第五片区2020-2021学年九年级上学期数学期末考试试卷
试卷更新日期:2021-12-15 类型:期末考试
一、单选题
-
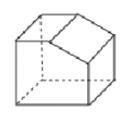
1. 计算2cos 30°的值为 ( )A、1 B、 C、 D、2. 如图所示的几何体,它的左视图是( )
 A、
A、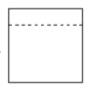 B、
B、 C、
C、 D、
D、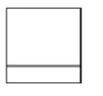 3. 若反比例函数 的图象位于第一、三象限,则m的取值范围是 ( )A、m<0 B、m>0 C、m< D、m>4. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )
3. 若反比例函数 的图象位于第一、三象限,则m的取值范围是 ( )A、m<0 B、m>0 C、m< D、m>4. 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为 的位似图形△OCD,则点C坐标( )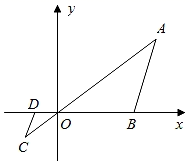 A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)5. 已知关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 ( )A、m≥2 B、m<2 C、m≥0 D、m<06. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A、(﹣1,﹣1) B、(﹣ ,﹣1) C、(﹣1,﹣ ) D、(﹣2,﹣1)5. 已知关于x的一元二次方程 有两个不相等的实数根,则m的取值范围是 ( )A、m≥2 B、m<2 C、m≥0 D、m<06. 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( ) A、4 B、3 C、4.5 D、57. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
A、4 B、3 C、4.5 D、57. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( ) A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<28. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<28. 某公司今年4月的营业额为2500万元,按计划第二季度的总营业额要达到9100万元,设该公司5、6两月的营业额的月平均增长率为x.根据题意列方程,则下列方程正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( ) A、 B、 C、 D、10. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )A、20 B、24 C、28 D、3011. 某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( )
A、 B、 C、 D、10. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )A、20 B、24 C、28 D、3011. 某数学兴趣小组来到城关区时代广场,设计用手电来测量广场附近某大厦CD的高度,如图,点P处放一水平的平面镜.光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=1.5米,BP=2米,PD=52米,那么该大厦的高度约为( ) A、39米 B、30米 C、24米 D、15米12. 反比例函数 和 在第一象限的图象如图所示,点A在函数 图象上,点B在函数 图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为( )
A、39米 B、30米 C、24米 D、15米12. 反比例函数 和 在第一象限的图象如图所示,点A在函数 图象上,点B在函数 图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
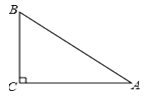
13. 已知一元二次方程 的一个根为0,则 .14. 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么sinA=.
 15. 如图,在 中, , 分别是边 , 的中点.若 的面积为 .则四边形 的面积为.
15. 如图,在 中, , 分别是边 , 的中点.若 的面积为 .则四边形 的面积为.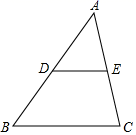 16. 如图,矩形OABC的顶点A,C分别在坐标轴上,A(8,0),D(5,7),点P是边AB或边OA上的一点,连接CP,DP,当△CDP为等腰三角形时,点P的坐标为.
16. 如图,矩形OABC的顶点A,C分别在坐标轴上,A(8,0),D(5,7),点P是边AB或边OA上的一点,连接CP,DP,当△CDP为等腰三角形时,点P的坐标为.
三、解答题
-
17. 解方程:18. 如图,在▱ABCD中,AE⊥BC于点E,CF⊥AB于点F,且AE=CF,求证:▱ABCD是菱形.
 19. 如图,在 中, , , ,求 的面积.
19. 如图,在 中, , , ,求 的面积.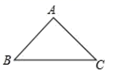 20. ETC( Electronic Toll Collection )不停车收费系统是目前世界上最先进的路桥收费方式.安装有ETC的车辆通过路桥收费站无需停车就能交纳费用.某高速路口收费站有A,B,C,D四个ETC通道,车辆可任意选择一个ETC通道通过,且通过每个ETC通道的可能性相同,一天,小李和小赵分别驾驶安装有ETC的汽车经过此收费站.(1)、求小李通过A通道的概率;(2)、请用列表或画树状图的方法表示出两人通过此收费站的所有可能结果,并求出小李和小赵经过相同通道的概率.21. 某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米.
20. ETC( Electronic Toll Collection )不停车收费系统是目前世界上最先进的路桥收费方式.安装有ETC的车辆通过路桥收费站无需停车就能交纳费用.某高速路口收费站有A,B,C,D四个ETC通道,车辆可任意选择一个ETC通道通过,且通过每个ETC通道的可能性相同,一天,小李和小赵分别驾驶安装有ETC的汽车经过此收费站.(1)、求小李通过A通道的概率;(2)、请用列表或画树状图的方法表示出两人通过此收费站的所有可能结果,并求出小李和小赵经过相同通道的概率.21. 某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米.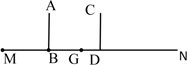 (1)、请在图中画出光源O点的位置,并画出O到MN的垂线段OH(不写画法);(2)、若小明身高1.5m,求OH的长.22. 某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低1万元时,平均每周能多售出2辆.该4S店要想平均每周的销售利润为96万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?23. 如图,△ABC是等边三角形,点D在AC上,连接BD并延长,与∠ACF的角平分线交于点E.
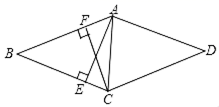
(1)、请在图中画出光源O点的位置,并画出O到MN的垂线段OH(不写画法);(2)、若小明身高1.5m,求OH的长.22. 某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低1万元时,平均每周能多售出2辆.该4S店要想平均每周的销售利润为96万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?23. 如图,△ABC是等边三角形,点D在AC上,连接BD并延长,与∠ACF的角平分线交于点E. (1)、求证:△ABD ∽△CED;(2)、若AB=8,AD=2CD,求CE的长.24. 如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.
(1)、求证:△ABD ∽△CED;(2)、若AB=8,AD=2CD,求CE的长.24. 如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.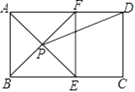 (1)、求证:四边形ABEF 是正方形;(2)、如果AB=6,AD=8,求tan∠ADP的值.25. 某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速 (千米/小时)与时间 (小时)成反比例函数关系缓慢减弱.
(1)、求证:四边形ABEF 是正方形;(2)、如果AB=6,AD=8,求tan∠ADP的值.25. 某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速 (千米/小时)与时间 (小时)成反比例函数关系缓慢减弱.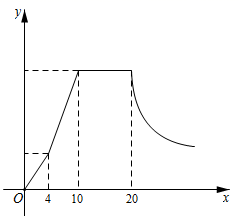 (1)、这场沙尘暴的最高风速是千米/小时,最高风速维持了小时;(2)、当 时,求出风速 (千米/小时)与时间 (小时)的函数关系式;(3)、在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.26. 如图所示,为了测量某矿山CH的高度,科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点,在A点,在A点观察H点的俯角为 ,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为 ,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据: )
(1)、这场沙尘暴的最高风速是千米/小时,最高风速维持了小时;(2)、当 时,求出风速 (千米/小时)与时间 (小时)的函数关系式;(3)、在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.26. 如图所示,为了测量某矿山CH的高度,科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点,在A点,在A点观察H点的俯角为 ,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为 ,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据: )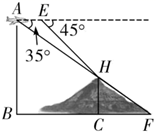 27. 如图,一次函数y=kx+b(k≠0)与反比例函数y= (a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,
27. 如图,一次函数y=kx+b(k≠0)与反比例函数y= (a≠0)的图象在第一象限交于A、B两点,A点的坐标为(m,4),B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C.若OC=CA,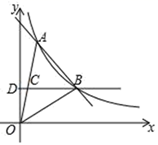 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、在直线BD上是否存在一点E,使得△AOE是以AO为直角边的直角三角形,直接写出所有可能的E点坐标.28. 如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、在直线BD上是否存在一点E,使得△AOE是以AO为直角边的直角三角形,直接写出所有可能的E点坐标.28. 如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.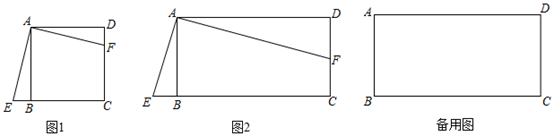 (1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.
(1)、如图1,若k=1,则AF与AE之间的数量关系是;(2)、如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)(3)、若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长.